Identification of methylation markers discriminating between CRC and normal blood

The protocol for marker selection with omic dataset 

Brief introduction

With the considerations of statistical principles, screening markers and candidates from thousands of the variables with a small sample set are difficult. This is because, in most cases, it could not meet the sufficient power for statistical inference after the multi-correction test step by control the false discovery rate. Therefore, for the purpose of translational research rather than a quite rigorous mathematical study, scientists for biological or medical research often applied heuristic strategies to narrow down the target list for experiments and validation in a larger cohort. The strategies include variance-based methods like information entropy, median absolute deviation and model-based method such as RandomForest, LASSO, GLM. Alternatively, people combine those methods to shrink the number of the marker list to a reasonable range for further study.    

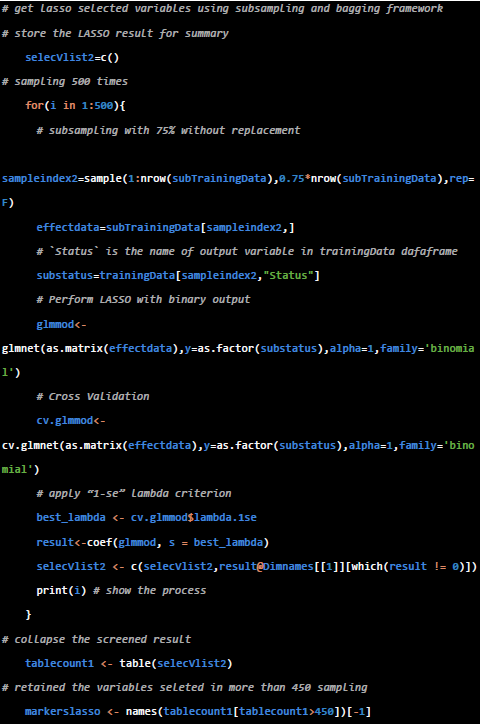
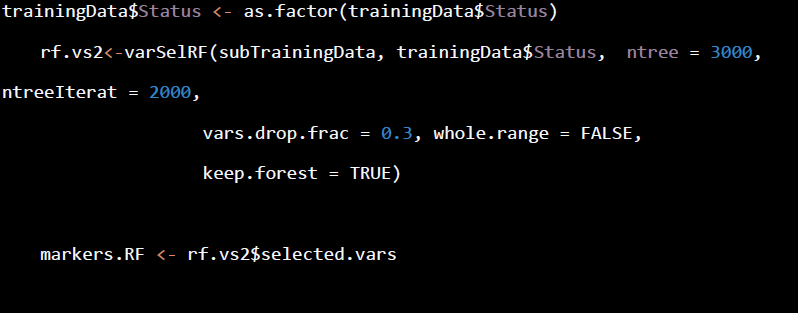
This protocol presents the code and a step-by-step procedure for performing RandomForest and LASSO analysis in marker selection section of our recent published work in Science Translational Medicine(1). In the supplementary of the paper, we summarized the procedure by “Two feature selection methods suitable for high-dimensionality on the prescreened were applied on the training dataset: Least Absolute Shrinkage and Selection Operator (LASSO) (2) and Random Forest based variable selection method using OOB error (3). For LASSO selection operator, we adopted an analysis of the “multi-split” strategy on data set as results can depend strongly on the arbitrary choice of a random sample split for sparse high-dimensional data (4). We subsampled 75 percent of the dataset without replacement 500 times and selected the markers with repeat occurrence frequency more than 450. The tuning parameters were determined according to the expected generalization error estimated from 10-fold cross-validation and information-based criteria AIC/BIC, and we adopted the biggest value of lambda such that the error was within one standard error of the minimum, known as “1-se” lambda. For the random forest analysis, using the OOB error as a minimization criterion, we carried out variable elimination from the random forest with dropping fraction of each iteration at 0.3. We then obtained nine overlapping methylation markers by the two methods for model building a binary prediction.” Here, we show the code for the readers who would like to apply this method in their own dataset.

• Input Dataset

The LASSO and RandomForest are both model-based methods, which require the dataset have both variable matrix (gene expression matrix, for instance) and output vector (binary, continuous or survival outcomes.) The matrix is denoted by represents the number of samples and the represents variable numbers. 

In our code, we marked the matrix by subTrainingData variables. The output vector was recorded as substatus. In this protocol, substatus was merged with subTrainingData into trainingData with the header of “Status”.

• Required packages and environment. 

All the analysis was performed under R environment. Before running the code, please make sure all the required packages were installed and loaded in the env. The code for load the packages are as follow: 

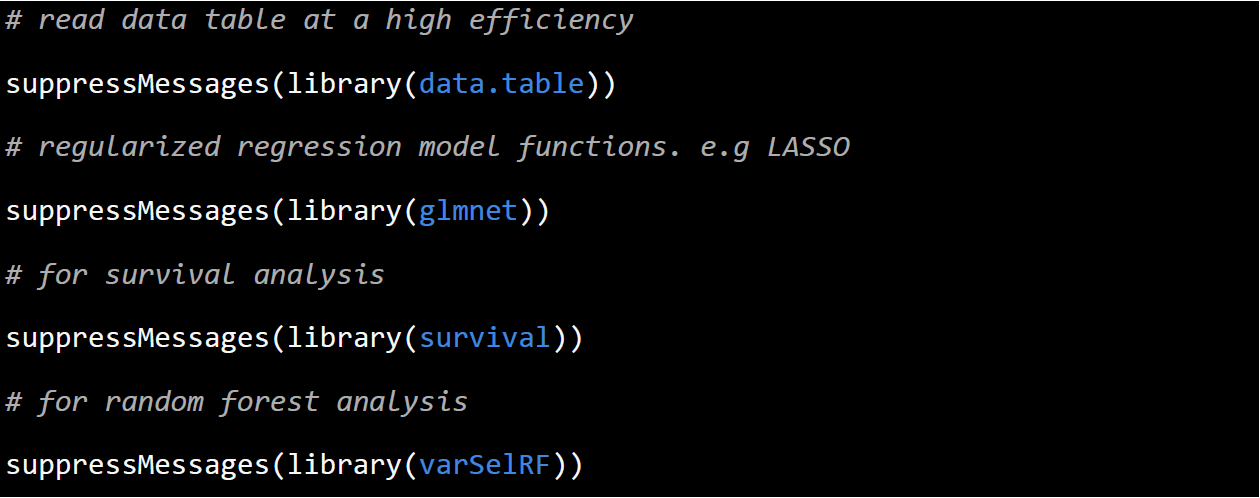
• LASSO-bagging procedure 

In our analysis, we introduced a bagging strategy on the dataset to weaken the dependency of the screen process to the training dataset.  We applied glmnet for the LASSO and manually run the resampling. To note, the sampling is a random process, please set the random seed by set.seed() function if you would like to reproduce the exactly result of the last running.  

• RandomForest procedure

LASSO is linear screening method. A non-linear screening method like RandomForest is also worth a run for the purpose. Here shows the code for Random Forest

• Get Overlapped markers with LASSO and random Forest

Keep the markers that were both screened by the LASSO and RandomForest methods

• SessionInfo()

Here is the SessionInfo() for running and testing this protocol.

For assistants, please contact Qi Zhao in Sun Yat-sen University Cancer Center by zhaoqi@sysucc.org.cn

1.         Luo, H., Zhao, Q., Wei, W., Zheng, L., Yi, S., Li, G., Wang, W., Sheng, H., Pu, H., Mo, H. et al. (2020) Circulating tumor DNA methylation profiles enable early diagnosis, prognosis prediction, and screening for colorectal cancer. Sci Transl Med, 12.

2.         Tibshirani, R. (1996) Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological), 267-288.

3.         Diaz-Uriarte, R. (2007) GeneSrF and varSelRF: a web-based tool and R package for gene selection and classification using random forest. BMC bioinformatics, 8, 328.

4.         Frank, E., Harrell, J., Kerry, L. and Daniel, B. (1996) Tutorial in biostatistics multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med, 15, 361-387.

Category