DEV analysis

Protocol for compute Dynamical Eigen-Value (DEV) using time series data.

Dynamical Eigen-Value (DEV) analysis

    The most critical step for the DEV approach is to reconstruct the attractor. As system dynamics may change through time, we employed a windowing approach. Thus, a proper window size, w, (i.e., length of time series segment for estimating DEV) needed to be chosen for each time series analysis, in order to best describe the associated dynamics of the system. In addition, best embedding dimension, E, and time lag, τ, needed to be estimated.

    In details, we screened for the parameter orchestration resulting in the best performance [i.e., S-map prediction skill]. To determine the optimal window size for computation, we screened various window sizes. For each window size, we evaluated S-map skill (predictability, ρ) for various combinations of embedding dimensions E (1 to 12) and time lags τ (1 to 12) and obtained the highest ρ (ρ_max). During this stage of searching the optimal window size, for simplifying the calculation, we chose θ = 0 in S-map. When θ = 0, S-map is equivalent to an autoregressive model of order E. The optimal window size (w) close to the plateau was determined visually, beyond which increasing the window size leads to very minor improvement of the predictability (Fig. 1a). Considering the paucity of time series data and avoiding the risk of overfitting, we chose the window size closest to the plateau phase. The best E and τ associated with the optimal window size resulting in best ρ were used throughout the analysis. Then, sensitivity analyses for various E, τ, and w should be done to ensure the robustness of results.

    After determining w, E, and τ, we proceeded to estimate the time series of Jacobian for the window segment (Fig. 1b, c & d). To account for changing nonlinearity of the reconstructed attractor, for each time series segment defined by the moving window, S-map analyses were run for various θ (0 to 2.5); the best θ giving the best S-map forecast skill was chosen. After obtaining the time series of Jacobian, we subsequently calculated the dominant eigen-value at each time point within the window. Then, we averaged all eigen-values derived in the time window as our DEV indicator. The averaging process smoothed out the uncertainty of estimating DEV at each time point; in addition, the averaged DEV indicated the vulnerability to critical transition for that region of attractor. Finally, moving the window forward and repeating the calculation for every time step, we obtained the time series of DEV. Absolute of DEV approaching 1 is indicative of critical transition. Using time series segments of the chosen window size, we consecutively estimated the early warning signals. The signals were reported and matched to the time index associated with the last point of the window. 

Computation:

    Documentation of all the analytical procedures and R codes for reproducing the results are provided in Zendo repository, https://doi.org/10.5281/zenodo.7379358. 

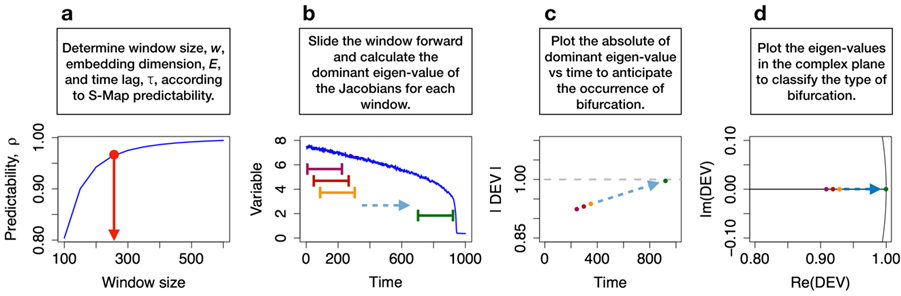
Figure 1. Schematic illustrating the procedures to estimate the time-varying dominant eigen-values that anticipate critical transition and classify types of bifurcation. To determine the optimal window size for computation, we screened different window sizes. For each window size, we evaluated S-map skill (predictability, ρ) for various combinations of embedding dimensions E (1 to 12) and time lags τ (1 to 12) and obtained the highest ρ (ρ_max). The optimal window size (w) close to the plateau was determined visually (a), beyond which increasing the window size lead to very minor improvement of the predictability.  The best E and τ associated with the optimal window size resulting in best ρ were used throughout the analysis. We then slid the window forward in time (b), and calculated and visualized DEV (c & d). Then, sensitivity analysis for various E, τ, and w should be done to ensure robustness of results.