- Submit a Protocol
- Receive Our Alerts
- Log in
- /
- Sign up
- My Bio Page
- Edit My Profile
- Change Password
- Log Out
- EN
- EN - English
- CN - 中文
- Protocols
- Articles and Issues
- For Authors
- About
- Become a Reviewer
- EN - English
- CN - 中文
- Home
- Protocols
- Articles and Issues
- For Authors
- About
- Become a Reviewer
Forest GPP Calculation Using Sap Flow and Water Use Efficiency Measurements
Published: Vol 7, Iss 8, Apr 20, 2017 DOI: 10.21769/BioProtoc.2221 Views: 9342
Reviewed by: Arsalan DaudiMarisa RosaSamik BhattacharyaAnonymous reviewer(s)

Protocol Collections
Comprehensive collections of detailed, peer-reviewed protocols focusing on specific topics
Related protocols

A Plate Growth Assay to Quantify Embryonic Root Development of Zea mays
Jason T. Roberts [...] David M. Braun
Oct 20, 2023 2224 Views
Detection and Quantification of Programmed Cell Death in Chlamydomonas reinhardtii: The Example of S-Nitrosoglutathione
Lou Lambert and Antoine Danon
Aug 5, 2024 1557 Views

Enzymatic Starch Quantification in Developing Flower Primordia of Sweet Cherry
Nestor Santolaria [...] Afif Hedhly
Apr 5, 2025 1861 Views
Abstract
This is a protocol to evaluate gross primary productivity (GPP) of a forest stand based on the measurements of tree’s sap flow (SF), 13C derived water use efficiency (WUE), and meteorological (met) data. GPP was calculated from WUE and stomatal conductance (gs), the later obtained from SF up-scaled from sampled trees to stand level on a daily time-scale and met data. WUE is obtained from 13C measurements in dated tree-ring wood and/or foliage samples. This protocol is based on the recently published study of Klein et al., 2016.
Keywords: TreesBackground
Forests play a major role in the terrestrial carbon cycle through CO2 assimilation and respiration, as well as on the Earth climate by influencing atmosphere CO2 concentration (Luyssaert et al., 2007; Bonan, 2008; Canadell and Raupach, 2008; Reichstein et al., 2013). Gross primary productivity (GPP), plants’ carbon uptake through photosynthesis, is the ultimate source of organic material in land biosphere in general and in food production in particular.
GPP at the ecosystem scale is mainly derived using the eddy covariance (EC) technique, as the difference between EC-measured net ecosystem CO2 exchange (NEE) and the daily inferred ecosystem respiration (Re). The latter one is obtained by extrapolating measured night-time NEE, which equals to ecosystem respiration, Re, to daytime based on empirical equations of Re response to temperature and soil humidity (Aubinet et al., 2000; Baldocchi, 2003; Reichstein et al., 2005; Grunzweig et al., 2009). However, the EC approach has several limitations and uncertainties. Its application is limited to relatively large homogeneous and flat terrains. EC technique is critically dependent on factors such as the system deployment in field (e.g., height above the canopy), on atmospheric conditions (e.g., turbulence conditions, advections) (Aubinet et al., 2000), on corrections applied to data processing programs and algorithms. A common way to assess EC measurements reliability is through the evaluation of the ‘energy closure’ over the measured ecosystem. This test indicates in most sites an energy gap of 20% or more (Foken, 2008). Empirical extrapolation of the night-time NEE measurement to approximate daytime Re has by itself significant uncertainties (e.g., Van Gorsel et al., 2009). NEE measurements provide a whole ecosystem flux only, thus explicit carbon uptake by trees cannot be distinguished from others ecosystem layers. EC measurements are also relatively expensive.
The current protocol describes an alternative method for calculation of forest trees GPP based on measurements of air temperature and humidity, trees’ sap flow (SF) rate and intrinsic water use efficiency (WUEi, the ratio A/gs), where A is the rate of photosynthetic CO2 assimilation and gs is stomatal conductance. This protocol is based on the recently published study of Klein et al., 2016. WUEi is a parameter characterizing plant species, with a seasonal variation (Seibt et al., 2008; Klein et al., 2013 and 2016). It can be calculated from the carbon isotope ratio (δ13C) in the assimilated carbon of plant tissues (Farquhar and Richards, 1984). This is combined with sap flow measurements, which can be obtained easier and at a lower cost than EC measurements, and often have less spatial limitations (independent on ecosystem footprint, topography, homogeneity, etc.), and enable GPP estimation in complex ecosystems. The method is applicable to calculate GPP of woody vegetation and can be considered as total ecosystem GPP if the contribution of understory layer to the total ecosystem GPP can be neglected (e.g., dry environments) or independently assessed. Note that using this approach can also be applied to archived SF and 13C data to reconstruct past variations in GPP, as long as these data are available.
Materials and Reagents
- Forest or woody stand, which can be assumed to be homogenous to facilitate scaling up to stand level
Note: If stand is composed of considerably different plots and species, the method can be applied separately for each plot. The measurements are conducted on living trees. No reagents are used in this procedure.
Equipment
- Tape measure of 2-3 m or caliper for tree diameter at breast height (approximately at 1.3 m, DBH, cm) distribution measurements
- A total station theodolite or at least 30-50 m long tape-measure and compass for establishing a sample plot(s) with known area in order to get stand density
- Sap flow sensors of any suitable type (e.g., EMS Brno, model: THB sensors ; or ICT International, model: HFD8-100 ; or UP, model: TDP sensors , etc.)
Note: The type of sensors depends on tree diameter, financial possibilities, power supply options etc. The most simple, TDP sensors can be manufactured in the institute workshop (see description, e.g., in Lu et al., 2004). - Dendrometers of any type for obtaining of seasonal DBH growth curve (e.g., EMS Brno, model: DRL26C or Natkon, model: Point Dendrometers [Oetwil am See, Switzerland])
- Thermometer and air moisture meter or automatic meteorological station for continuous data recording
- Datalogger for storing sap flow and met’ data (if no own logger is provided by SF and met’ sensors suppliers), e.g., (Campbell Scientific, model: CR1000 ). Most of factory-made sap flow sensors are supplied with own loggers (e.g., EMS Brno, Czech Republic)
- Incremental borer. Short, 5.15’’ borers would usually fit for obtaining wood formed in the recent decade or period of interest
- Equipment for tree rings analysis
Note: Best would be professional dendrometry desk station. Microtome can also help for intra-annual slicing. But the wider the tree-rings are, the easier it is to slice them with scalpel alone. - Laboratory for δ13C analysis
Note: This can be done in house isotope ratio mass spectrometry, or by commercial IRMS service labs.
Procedure
Note: The technology of SF measurements and up-scaling from measuring point to tree is not discussed in this protocol. The theory and practice of SF measurements is discussed, e.g., in Čermák et al., 2004; Lu et al., 2004; Tatarinov et al., 2005, as well as in user guides of particular SF sensors. Furthermore, it is assumed that continuous data of SF of single trees in L h-1 tree-1 are available. Similarly, the protocol does not discuss δ13C isotopic analysis of wood material.
- Select representative sample plot, measure its area and DBH of all sample trees within the plot. For small trees or shrubs instead of breast height it is possible to measure diameter at lower level, e.g., at 10 cm. In any case, diameter should be measured and SF sensors should be installed below the first living branch (for shrubs, when branching starts from the ground, each branch should be considered as separate stem). The plot size depends on woody plant species variability, stand density and DBH variability, with more sparse and variable stands requiring larger plot area. We recommend that the plot should include about 50-150 trees in order to get reliable DBH distribution. For multi-species stands the researcher should first evaluate the possible contribution of each species to the total stand GPP (e.g., its proportion of the total stand basal area/LAI/crown area, taking into account, if possible, its photosynthesis rate relatively to other species, on the basis of data from literature or chamber measurements) before deciding how to distribute sensors among species (taking into account financial limitations of total amount of sensors). However, this is a special topic beyond the scope of this protocol. For more details about sampling size see, e.g., Kish, 1965.
- Select sample trees for SF measurement within the plot according to DBH distribution. Sample trees should be representative of the stand and include the entire DBH range. The total number of sample trees depends on the DBH range, stand species composition, desired precision and financial constraints. J. Cermak proposed to select sample trees using so called quantiles of total method, when total set of trees at sample plot is sorted according to a certain biometrical parameter B (usually DBH or basal area) in ascending order and cumulative B is calculated simultaneously. See details on sampling strategy, e.g., in Čermák et al., 2004 and 2014. Good description of sampling strategy is also given in ICT booklet Sap flow installation scenarios.
Install SF sensors on selected sample trees. Installation procedure is described in user guides of particular sensors. See more information, e.g., in Čermák et al., 2004 and 2014; Paudel et al., 2013. - Install dendrometers on the trees which will be used for δ13C sampling. The number of trees for δ13C sampling depends on the level of variance in the plot. For statistical reasons, n = 30 is usually used. But often not all SF sensors are functional and hence we ended up using a lower number for our analysis. But 30 trees is a good recommendation. Optimally, one should use the same trees as for SF measurements, and these must represent the plot. If possible, stem growth should be monitored in all study trees. This is feasible using simple girth-tapes which hare monitored at least once a week.
- Measure SF and met data continuously (1/2 hourly) during the study period. Meteorological data (air temperature, Ta, and moisture, RH) should be best measured in the middle of the canopy foliage layer.
- Take plant material samples for 13C analysis
- For further GPP calculation, SF and WUEi values for the same time periods are required. Consequently, the time of formation of the plant organs samples for 13C analysis should be known at the best time resolution (monthly or weekly, then the values should be interpolated in order to get daily values for the whole period of analysis), as it determines the time resolution of WUEi calculation.
- Time resolution can be obtained in several ways.
- Wood samples should be taken from tree rings. Identifying the period of formation of specific tree-ring sub-sections could be allowed by calibration to an empirical stem growth curve from contemporary dendrometer data. Points along this curve (y-axis) were then applied to the observed growth curve to extract the estimated date of formation (x-axis) (Klein et al., 2016, see Figure 1).
- In some ecosystems, the period of stem growth can be lagged after the period of foliage growth. For periods when no stem growth occurs, but foliage or shoots growth takes place, leaf or shoot samples should be taken (see Figure 1). Leaf or needle samples can be dated in the same way as tree ring samples, by means of regular measurements of needles or leaves length (see Klein et al., 2005).
- If there is a dormancy period (e.g., winter in boreal zone), no sampling is necessary, as no GPP occurred.
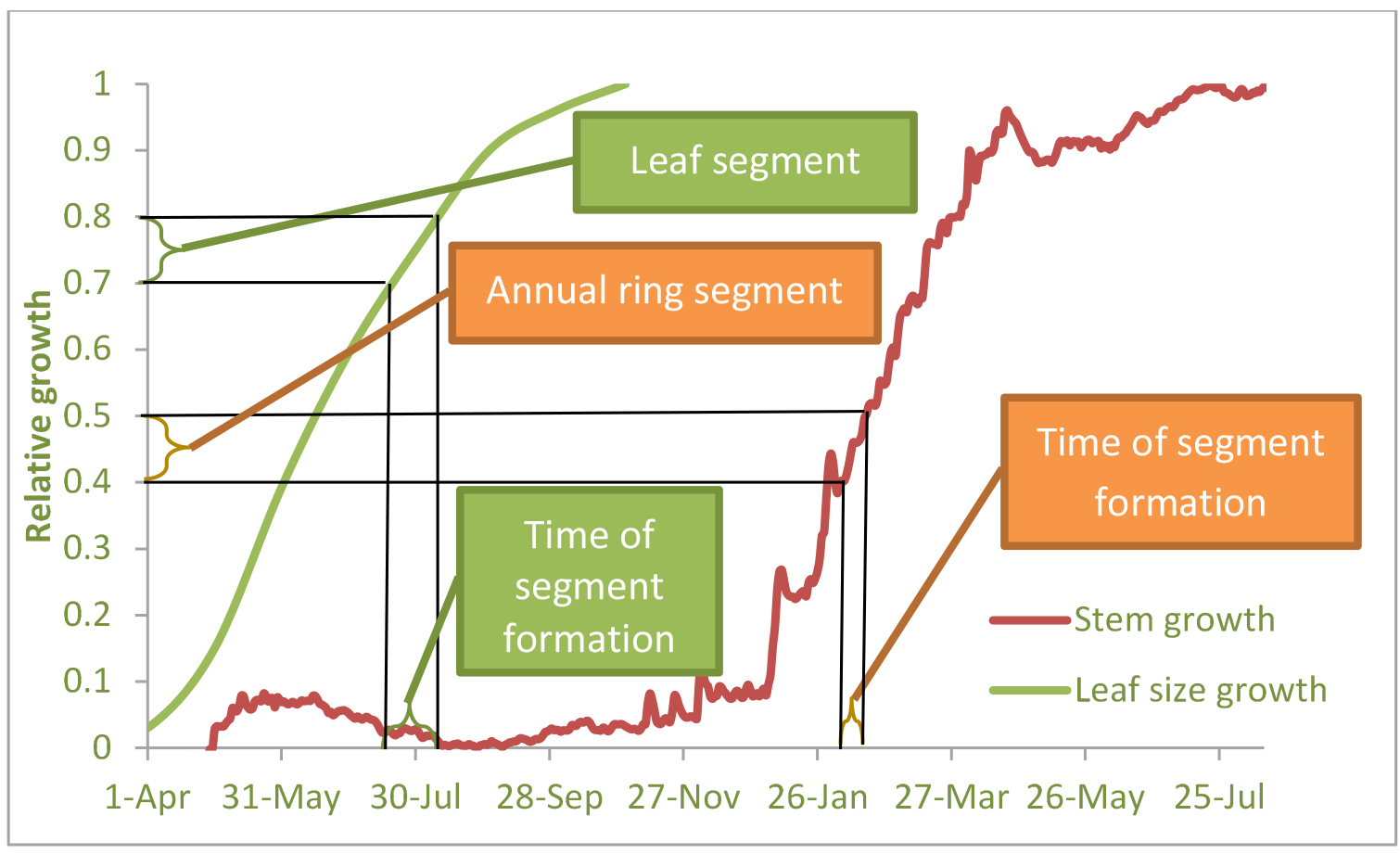
Figure 1. Scheme of high-resolution ring width development and leaf/needle elongation with time, and the sample slices dating. Example from Yatir semi-arid pine forest, Israel (see Maseyk et al., 2008) - 13C analysis should be made on the plant samples (tree ring sections and/or leaf samples) and attributed to particular time intervals.
Data analysis
- The estimation of GPP is based on the well-established physiological relationship: WUEi = A/gs (μM CO2 mol-1 H2O). Assuming that for a good approximation, stand assimilation - Astand = GPP (in reality, A = GPP - RL; where RL is daytime leaf respiration and is usually a minor component of Re) and GPP is usually estimated using nighttime EC measurements extrapolated to the daytime (Reichstein et al., 2005). We use the following main estimate for GPP at time period t:
GPP (t) = WUEi(t)/gs(t) (1)
which can be solved by obtaining independent estimates of WUEi and gs. - WUEi is estimated from δ13C measurements of organic material averaged from all samples taken at the same growing time interval t, using the following equation (adapted from Farquhar and Richards 1984; Seibt., 2008):
WUEi(t) = Ca(t)/r x {[b - Δ - pr x (Γ*/Ca(t))]/[b - a + (b - am) x (gs/(r x gi))]} (2)
where,
Ca is the atmospheric CO2 concentration in ppm (continuously measured on site, as it is not varying or taken as period average from the nearby station where it is measured),
r is the ratio of the diffusivities of CO2 and water vapor in air (1.6),
a, am, b and pr are the leaf-level discriminations against 13C in the diffusion through the stomata (4.4‰), during dissolution and liquid phase diffusion (1.8‰), in biochemical CO2 fixation (29‰), and in photo-respiratory CO2 release (8‰), respectively,
Δ is the tree discrimination against 13C,
Γ* is the temperature-dependent CO2 compensation point of ca. 30-45 ppm at our site (Maseyk et al., 2008),
gs/gi is the ratio between stomatal and internal conductance to CO2 respectively (0.5 according to Maseyk et al., 2011). The values above are valid for plants in general, but they can vary, and the best approach would be to test it for the species of study or use best estimate for the most phylogenetically close species. The tree discrimination against 13C (Δ) is calculated as follows:
Δ = (δ13Ca - δ13Co)/(1 + δ13Co) (3)
where, δ13C = (δ13C/δ12C)sample/(δ13C/δ12C)reference - 1 and the reference is Vienna-PDB (Coplen, 1994), and subscripts a and o stand for atmospheric air (at annual resolution) and the organic material (tree-ring or needle), respectively. WUEi from Eq.3 is representative for the period of δ13C signal deposition (depending on time resolution of plant sample formation dating; Ca should be averaged for the same period). WUEi values for intermediate days between δ13C measurements could be interpolated. - Stomatal conductance gs(t) for Eq.1 (as daytime average) can be calculated from measured stand transpiration and continuously monitored VPD(t) (average daytime, daily) using the general relationship (Beer et al., 2009):
gs(t) = T(t)/VPD(t) (4)
T(t) was measured as sap flow (SF) of individual trees integrated over the daily cycle (to overcome possible time offsets between SF and T, which can reach up to a few hours, e.g., under dry conditions) and up-scaled to stand level as described below. Vapor pressure deficit (VPD) can be calculated as follows (see, e.g., Monteith and Unsworth, 2007):
where, VPD(t) is in Pascals and RH (in %) and Ta (in °C) are air humidity and temperature, respectively. VPD is daytime averaged since CO2 uptake is restricted to daytime hours only. If other conditions preventing CO2 uptake for the particular species/region are known (too high or too low VPD or air temperature etc.), the VPD records corresponding to such conditions should be also excluded from averaging.
As mentioned above, we assume that although a time offset between SF and T of up to few hours can occur on the daily scale, stand transpiration total T is equal to total daily stand sap flow total (SFstand). As GPP is restricted to daytime, T should be restricted to same period, thus since water storage depleting and refilling acquired daily at a tree level, but night time T is negligible it is assumed that daily SF equals daytime T. Several possible SF up-scaling procedures from tree to stand level are available. (1) Dependence of tree SF on DBH can be derived by means of linear or nonlinear regression (where SF(t) is expressed in L tree-1 day-1) for each particular day and then
T(t) = SFstand(t) = ∑kSF(t, Dk) × nk (6)
where,
T(t) is expressed in mm day-1,
Dk and nk are mean DBH of DBH class k and stocking density (trees ha-1) of trees of this diameter class (Čermák et al., 2004). (2) Another option is to calculate sap flux density per unit sapwood cross-section area averaged among sample trees, (SFD(t)) (in cm3 cm-2 day-1) and then multiply it by total stand sapwood area (∑SWA, in cm2 ha-1, see Klein et al., 2014):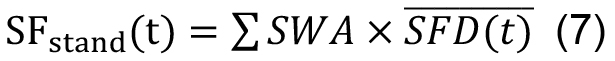
In addition, an evaluation of sapwood depth of the particular tree species is required, which can be measured separately or taken from the literature (see, e.g., Cermak and Nadezhdina, 1998; Gebauer et al., 2008). Then SWA of a particular tree can be calculated as follows: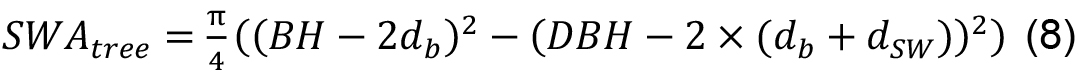
where, db and dSW are bark and sapwood widths, respectively. Then stand SWA can be calculated as the sum of sapwood areas of all trees on the sample plot divided by plot area.
We recommend to use the first method if there is expressed dependence of SFD on DBH and the second one if such dependence is missing (Tatarinov et al., 2015).
Finally, substituting WUEi from Eq.2 and gs calculated in daily scale by Eq.4 using Eqs. 5-8 into Eq.1 gives us daily GPP total.
The total analysis scheme is presented in Figure 2. An example of the protocol application is described by Klein et al., 2016.
Figure 2. Diagram of the protocol of forest GPP Calculation Using Sap Flow and Water Use Efficiency
Notes
- Weaknesses and uncertainties
- Sap flow measurements have their own sources of uncertainties related, e.g., to sapwood depth, SF radial profile, SF variation around stem, changing of sapwood physical properties with shrinkage/swelling etc. Preliminary information of sapwood depth is usually necessary for sensors installation. These data are generally species-specific and can be found in the literature. The problems and tips of sap flow measurements are discussed, e.g., in Čermák et al., 2004 and 2014; Paudel et al., 2013.
- The method is applicable for plants where sap flow sensors can be applied, i.e., mainly woody plants. Generally, it could be fully grown trees, but also young trees or shrubs, but this may require particular type of sensors (see, e.g., at http://emsbrno.cz/p.axd/en/Sap.Flow.small.stems.html). The method is not applicable for grasslands and small shrubs. Whereas in the forests with negligible understory layer the method should give total ecosystem GPP evaluation, in the presence of significant understory layer the result should be interpreted as GPP of trees only.
- Another limitation of the method concerns the time of formation of plant material used for the 13C analysis (which depends on the temporal resolution of measurement plus the slicing resolution and using standard techniques is weekly at best). The method is inapplicable for periods with no detectable growth of woody tissues or foliage observed.
- Additional source of uncertainty is the variability of Ta and RH within canopy, both, vertically and radially (with the distance from leaf surface), which influences VPD estimation. Generally, VPD at the leaf surface should be somewhat lower than VPD in the canopy air, which could lead to a certain overestimation of gs and consequently to the underestimation of GPP.
- Finally, the possible errors due to approximation of GPP = Astand should be assessed (which usually are negligible).
Acknowledgments
The protocol was adapted from Klein et al., 2016. This research was supported by the Jewish National Fund (KKL-JNF), the C. Wills and R. Lewis program in Environmental Science, German Research Foundation (DFG) as part of the project ‘Climate feedbacks and benefits of semi-arid forests (CliFF)’ and Israeli Science Foundation (ISF, grant 673/12 ‘Estimating gross photosynthesis using coupled COS/CO2 measurements at the ecosystem scale’).
References
- Aubinet, M., Grelle, A., Ibrom, A., Rannik, U. and Moncrieff, J. (2000). Estimates of the net carbon and water exchange of forests: the EUROFLUX methodology. In: Fitter, A. and Raffaeli, D. (Eds.). Advances in ecological research 30. Academic Press, pp: 113-175.
- Baldocchi, D. D. (2003). Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: past, present and future. Global Change Biol 9: 479-492.
- Beer, C., Ciais, P., Reichstein, M., Baldocchi, D., Law, B. E., Papale, D., Soussana, J-F., Amman, C., Buchmann, N., Frank, D. D. Gianelle, Janssens, I. A., Knohl, A., Köstner, B., Moors, E., Roupsard, O., Verbeeck, H., Vesala, T., Williams, C. A. and Wohlfahrt, G. (2009). Temporal and among-site variability of inherent water use efficiency at the ecosystem level. Global Biogeochem Cycles 23: GB2018.
- Bonnan, G. B. (2008). Forests and climate change: forcings, feedbacks, and the climate benefits of forests. Science 320(5882):1444-1449.
- Canadell, J. G. and Raupach, M. R. (2008). Managing forests for climate change mitigation. Science 320(5882): 1456-1457
- Čermák, J., Kučera, J. and Nadezhdina, N. (2004). Sap flow measurements with some thermodynamic methods, flow integration within trees and scaling up from sample trees to entire forest stands. Trees 18: 529-546.
- Čermák, J. and Nadezhdina, N. (1998). Sapwood as the scaling parameter- defining according to xylem water content or radial pattern of sap flow? Ann For Sci 55(5): 509-521.
- Čermák, J., Nadezhdina, N., Trcala, M. and Simon, J. (2014). Open field-applicable instrumental methods for functional assessment of whole trees and stands. iForest 8: 226-278.
- Coplen, T. B. (1994). Reporting of stable hydrogen, carbon, and oxygen isotopic abundances. Pure Applied Chem 66(2): 273-276.
- Farquhar, G. D. and Richards, R. A. (1984). Isotopic composition of plant carbon correlates with water-use efficiency of wheat genotypes. Functional Plant Biology 11: 539-552.
- Foken, T. (2008). The energy balance closure problem: an overview. Ecol Appl 18(6): 1351-1367.
- Gebauer, T., Horna, V. and Leuscher, C. (2008). Variability in radial sap flux density patterns and sapwood area among seven co-occurring temperate broad-leaved tree species. Tree Physiol 28(12): 1821-183.
- Grünzweig, J. M., Hemming, D., Maseyk, K., Lin, T., Rotenberg, E., Raz-Yaseef, N., Falloon, P. D. and Yakir, D. (2009). Water limitation to soil CO2 efflux in a pine forest at the semiarid “timberline”. J Geophys Res: Biogeosciences 114.
- Kish, L. (1965). Survey Sampling. Wiley, pp: 643.
- Klein, T., Hemming, D., Lin, T., Grünzweig, J. M., Maseyk, K. S., Rotenberg, E. and Yakir, D. (2005). Association between tree-ring and needle delta C-13 and leaf gas exchange in Pinus halepensis under semi-arid conditions. Oecologia 144: 45-54.
- Klein, T., Rotenberg, E., Cohen-Hilaleh, E., Raz-Yaseef, N., Tatarinov, F., Preisler, Y., Ogee, J., Cohen, S. and Yakir, D. (2014). Quantifying transpirable soil water and its relations to tree water use dynamics in a water-limited pine forest. Ecohydrology 7:409-419.
- Klein, T., Rotenberg, E., Tatarinov, F. and Yakir, D. (2016). Association between sap flow-derived and eddy covariance-derived measurements of forest canopy CO2 uptake. New Phytol 209(1): 436-446.
- Klein, T., Shpringer, I., Fikler, B., Elbaz, G., Cohen, S. and Yakir, D. (2013). Relationships between stomatal regulation, water-use, and water-use efficiency of two coexisting key Mediterranean tree species. Forest Ecol Manag 302: 34-42.
- Lu, P., Urban, L. and Zhao, P. (2004). Granier’s thermal dissipation probe (TDP) method for measuring sap flow in trees: Theory and practice. Acta Botanica Sinica 46(6):631-646.
- Luyssaert, S., Inglima, I., Jung, M., Richardson, A. D., Reichstein, M., Papale, D., Piao, S. L., Schulze, E.-D., Wingate, L., Matteucci, G., Aragao, L., Aubinet, M., Beer, C., Bernhofer, C., Black, K. G., Bonal, D., Bonnefond, J.-M., Chambers, J., Ciais, P., Cook, B., Davis, K. J., Dolman, A. J., Gielen, B., Goulden, M., Grace, J., Granier, A., Grelle, A., Griffis, T., Grünwald, T., Guidolotti, G., Hanson, P. J., Harding, R., Hollinger, D. Y., Hutyra, L. R., Kolari, P., Kruijt, B., Kutsch, W., Lagergren, F., Laurila, T., Law, B. E., le Maire, G., Lindroth, A., Loustau, D., Malhi, Y., Mateus, J., Migliavacca, M., Misson, L., Montagnani, L., Moncrieff, J., Moors, E., Munger, J. W., Nikinmaa, E., Ollinger, S. V., Pita, G., Rebmann, C., Roupsard, O., Saigusa, N., Sanz, M. J., Seufert, G., Sierra, C., Smith, M.-L., Tang, J., Valentini, R., Vesala, T. and Janssens, I. A. (2007). CO2 balance of boreal, temperate, and tropical forests derived from a global database. Global Change Biol 13: 2509-2537.
- Maseyk, K., Hemming, D., Angert, A., Leavitt, S. W. and Yakir, D. (2011). Increase in water-use efficiency and underlying processes in pine forests across a precipitation gradient in the dry Mediterranean region over the past 30 years. Oecologia 167(2): 573-585.
- Maseyk, K. S., Lin, T., Rotenberg, E., Grunzweig, J. M., Schwartz, A. and Yakir, D. (2008). Physiology-phenology interactions in a productive semi-arid pine forest. New Phytol 178(3): 603-616.
- Monteith, J. L. and Unsworth, M. H. (2007). Section 2.1. Gas and water vapor. In: Monteith, J. L. and Unsworth, M. H. (Eds.). Principles of environmental physics. 3rd edition. Academic Press, pp: 440.
- Paudel, I., Kanety, T. and Cohen, S. (2013). Inactive xylem can explain differences in calibration factors for thermal dissipation probe sap flow measurements. Tree Physiol 33(9): 986-1001.
- Reichstein, M., Bahn, M., Ciais, P., Frank, D., Mahecha, M. D., Seneviratne, S. I., Zscheischler, J., Beer, C., Buchmann, N., Frank, D. C., Papale, D., Rammig, A., Smith, P., Thonicke, K., van der Velde, M., Vicca, S., Walz, A. and Wattenbach, M. (2013). Climate extremes and the carbon cycle. Nature 500(7462): 287-295.
- Reichstein, M., Falge, E., Baldocchi, D., Papale, D., Aubinet, M., Berbigier, P., Bernhofer, C., Buchmann, N., Gilmanov, T., Granier, A. Grünwald, T., Havránková, K., Ilvesniemi, H., Janous, D., Knohl, A., Laurila, T., Lohila, A., Loustau, D., Matteucci, G., Meyers, T., Miglietta, F., Ourcival, J.-M., Pumpanen, J., Rambal, S., Rotenberg, E., Sanz, M., Tenhunen, J., Seufert, G., Vaccari, F., Vesala, T., Yakir, D. and Valentini, R. (2005). On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm. Global Change Biology 11: 1424-1439.
- Seibt, U., Rajabi, A., Griffiths, H. and Berry, J. A. (2008). Carbon isotopes and water use efficiency: sense and sensitivity. Oecologia 155(3): 441-454.
- Tatarinov, F. A., Kucera, J. and Cienciala, E. (2005). The analysis of physical background of tree sap flow measurement based on thermal methods. Meas Sci Technol 16: 1157-1169.
- Tatarinov, F., Preisler, Y., Rohatyn, S. and Yakir, D. (2015). Comparison of different tree sap flow up-scaling procedures using Monte-Carlo simulations. GRA 17: EGU2015-9151.
- Van Gorsel, E., Delpierre, N., Leuning, R., Black, A., Munger, J. W., Wofsy, S., Aubinet, M., Feigenwinter, C., Berniger, J., Bonal, D. and Chen, B. (2009). Estimating nocturnal ecosystem respiration from the vertical turbulent flux and change in storage of CO2. Agr Forest Meteorol 149: 1919-1930.
Article Information
Copyright
© 2017 The Authors; exclusive licensee Bio-protocol LLC.
How to cite
Tatarinov, F., Rotenberg, E., Yakir, D. and Klein, T. (2017). Forest GPP Calculation Using Sap Flow and Water Use Efficiency Measurements. Bio-protocol 7(8): e2221. DOI: 10.21769/BioProtoc.2221.
Category
Plant Science > Plant physiology > Abiotic stress
Plant Science > Plant physiology > Plant growth
Do you have any questions about this protocol?
Post your question to gather feedback from the community. We will also invite the authors of this article to respond.
Share
Bluesky
X
Copy link