- Submit a Protocol
- Receive Our Alerts
- Log in
- /
- Sign up
- My Bio Page
- Edit My Profile
- Change Password
- Log Out
- EN
- EN - English
- CN - 中文
- Protocols
- Articles and Issues
- For Authors
- About
- Become a Reviewer
- EN - English
- CN - 中文
- Home
- Protocols
- Articles and Issues
- For Authors
- About
- Become a Reviewer
Ionization Properties of Phospholipids Determined by Zeta Potential Measurements
Published: Vol 6, Iss 22, Nov 20, 2016 DOI: 10.21769/BioProtoc.2030 Views: 14848
Reviewed by: Marc-Antoine SaniFernanda SalvatoAnonymous reviewer(s)

Protocol Collections
Comprehensive collections of detailed, peer-reviewed protocols focusing on specific topics
Related protocols

Computational Analysis of Plasma Lipidomics from Mice Fed Standard Chow and Ketogenic Diet
Amy L. Seufert [...] Brooke A. Napier
Sep 20, 2023 2607 Views

Quantitative Determination of Cholesterol Hydroxylase Specificities by GC–MS/MS in Living Mammalian Cells
Hodaka Saito [...] Yoshio Yamauchi
Jan 20, 2024 2369 Views

A New Approach to Detect and Semi-quantify All Molecular Species and Classes of Anionic Phospholipids Simultaneously in Plant Samples
Manon Genva [...] Laetitia Fouillen
Apr 20, 2025 1718 Views
Abstract
Biological membranes are vital for diverse cellular functions such as maintaining cell and organelle structure, selective permeability, active transport, and signaling. The surface charge of the membrane bilayer plays a critical role in these myriad processes. For most biomembranes, the surface charge of anionic phospholipids contributes to the negative surface charge density within the interfacial region of the bilayer. To quantify surface charge, it is essential to understand the proton dissociation behavior of the titratable headgroups within such lipids. We describe a protocol that uses model membranes for electrokinetic zeta potential measurements coupled with data analysis using Gouy-Chapman-Stern formalism to determine the pKa value of the component lipids. A detailed example is provided for homogeneous bilayers composed of the monoanionic lipid phosphatidylglycerol. This approach can be adapted for the measurement of bilayers with a heterogeneous lipid combination, as well as for lipids with multiple titratable sites in the headgroup (e.g., cardiolipin).
Background
Phospholipids are central building blocks of biological membranes (Figure 1). As amphipathic molecules, each contains a hydrophobic region consisting of acyl chains and a hydrophilic region consisting of a polar headgroup (Figure 1A). Some phospholipid headgroups are zwitterionic, containing both positively and negatively charged functional groups at physiological pH (Figure 1B), whereas others are acidic, bearing an overall formal negative charge (Figure 1C). Lipids within biomembranes exist stably as a lamellar assembly, forming bilayers in which the acyl chains of two leaflets interact to form a hydrophobic core and two interfacial regions consisting of the polar headgroups (Figure 1D). Most naturally occurring biomembranes contain a certain percentage of acidic phospholipids; therefore, their lipid composition imparts a net negative charge to the interfacial region (Gennis, 1989; Marsh, 2013). Bilayer surface charge is a key factor in many membrane-level processes including interactions with proteins and solution ions as well as membrane morphology, fusion and phase changes. Because the formal charge of lipid headgroups is a primary determinant of this surface charge, it is critical to have accurate measurements of the proton dissociation behavior (quantified as pKa values) of the constituent functional groups.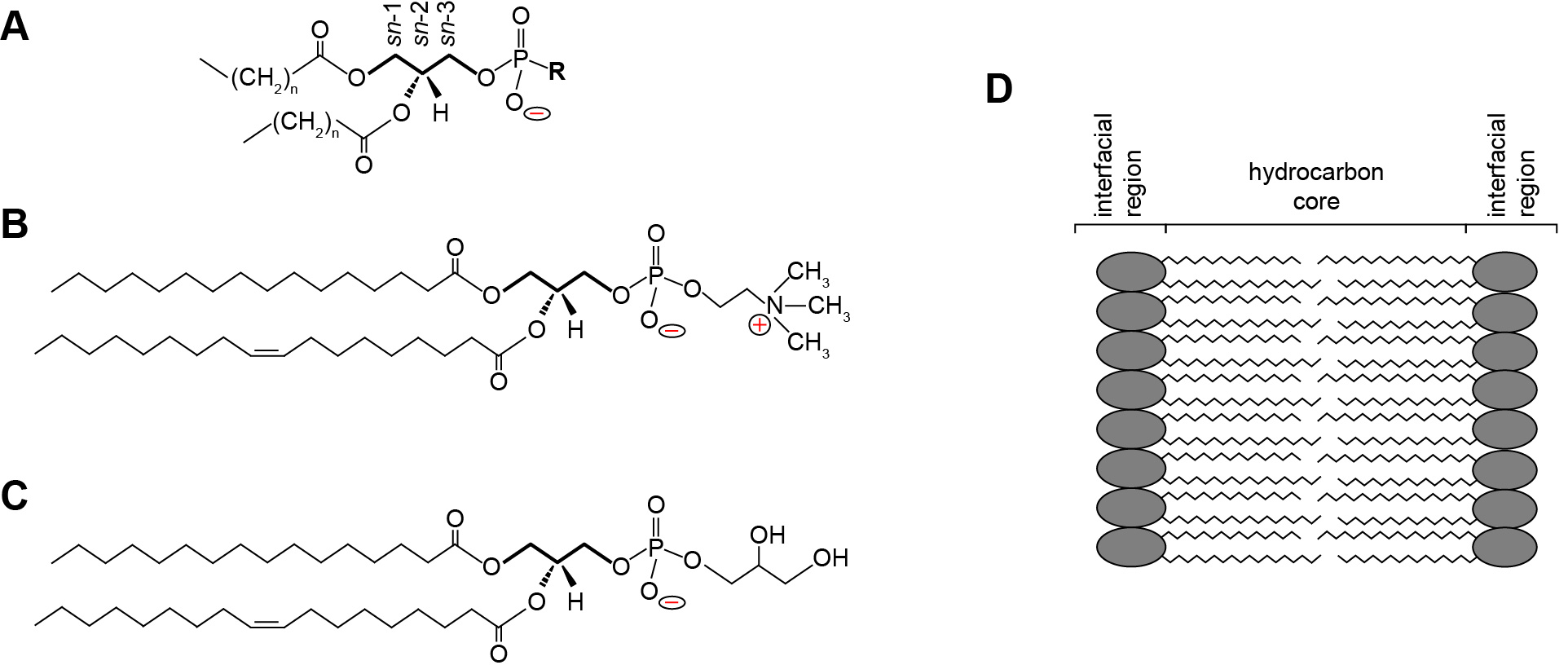
Figure 1. Phospholipid structure and the lamellar lipid bilayer. A. General structure of a glycerophospholipid. A common phospholipid is based on a scaffold of a central glycerol molecule (thickened line), with the constituent carbons designated by stereospecific numbering (sn-1, sn-2 and sn-3, as indicated). The hydrophobic domain consists of hydrocarbon tails esterified at the sn-1 and sn-2 positions. The polar headgroup contains a negatively charged phosphate group attached to the sn-3 position, which may be modified by an R group to render specific headgroup identity. B. Structure of phosphatidylcholine (R = choline) with a saturated 16 carbon aliphatic tail at the sn-1 position and an unsaturated 18 carbon tail at the sn-2 position. The zwitterionic nature of the headgroup is shown as the negative phosphate and the positive tertiary amine. C. Structure of phosphatidylglycerol (R = glycerol) with acyl chains identical to those shown above. The anionic nature of the headgroup is shown by the uncompensated negative charge on the phosphate. D. The lamellar lipid bilayer, showing the hydrocarbon core composed of the aliphatic lipid tails and the solvent-exposed interfacial regions.
The electric field that is established by charged headgroups results in a complex profile of electric potential in the aqueous region (Figure 2) (McLaughlin, 1977). Models for the electric potential profile are based on the physical chemistry of phase boundary interfaces, here representing a solid surface in contact with an aqueous phase (Oshima, 2010). Membrane surface electrostatics can be quantitatively modeled using Gouy-Chapman-Stern theory, which relates the density of charges on the membrane surface (σ, C m-2) and the electric potential (ψ, V), as described in the data analysis section. In a simplified model, the surface charge is comprised of charges that are fixed to the solid body as well as solution ions that are adsorbed tightly to the surface by chemical interactions. For lipid bilayers, the fixed charges can be considered to be the titratable acidic (phosphate) and basic (primary anime) functional groups of lipid headgroups, whereas the adsorbed ions are solution electrolytes that specifically bind headgroup sites with nonzero association constants (Tocanne and Teissie, 1990). This layer of charges is collectively defined as the Stern layer, but may be subdivided into other layers with increasing complexity. Adjacent to this region is a layer in which solvated solution ions are more diffusely distributed. In this region, termed the Gouy-Chapman layer, the distribution of counterions (those with charges opposite to the dominant surface charge) and coions (those with charges identical to the surface charge) arises from electrostatic attraction (counterions) or repulsion (coions) balanced with the entropic tendency of ions to diffuse away from the surface. Because counterions are highly enriched in this region due to electrostatic attraction to the surface, they act to screen the surface charge, thereby attenuating the electric field. Taken as a whole, this distribution of charges sets up the ‘diffuse electrical double layer’ of biomembranes.
Here we describe a methodology to determine the pKa of lipid headgroups using measurements of the electrostatic potentials of model membranes. This approach is based on the electrophoresis of lipid bilayer vesicles (liposomes), which we used in a recent publication to measure the proton dissociation behavior of the dimeric phospholipid cardiolipin (Sathappa and Alder, 2016). In the presence of an applied electric field, charged colloidal particles will migrate relative to the suspending liquid toward the electrode of opposing charge (Delgado et al., 2007). As the charged particle surface flows tangentially along the bulk fluid, there exists a thin layer of solution, termed the hydrodynamically stagnant layer, which moves with the particle. This layer extends into the diffuse region to a so-called slipping plane or shear plane. The electric potential at this layer that separates the hydrodynamically immobile layer from the bulk is termed the zeta potential (ζ) (Figure 2). The speed of migration depends on the electrophoretic mobility (μ, m2 V-1 s-1) of the particle, defined by the Helmholtz-Smoluchowski equation as the particle velocity per unit electric field:![]()
Where, εr is the relative permittivity, ε0 is the permittivity of free space, and η is the viscosity of the solution (Aveyard and Haydon, 1973). As Eq. 1 shows, the mobility of charged particles in an external electric field is directly related to the magnitude of ζ. Hence, in an electrolyte solution of a given pH, liposomes with greater surface charge will have a higher ζ and therefore move with higher velocity in a given electric field.
Whereas optical electrophoresis measurements provide an unambiguous measure of electrokinetic mobility and zeta potential, translating these measurements into information on proton dissociation characteristics of titratable groups requires more detailed evaluation. This protocol explains the preparation of suitable model membranes, measurements of zeta potential using optical electrophoresis, and data analysis using Gouy-Chapman-Stern formalism to obtain lipid pKa values.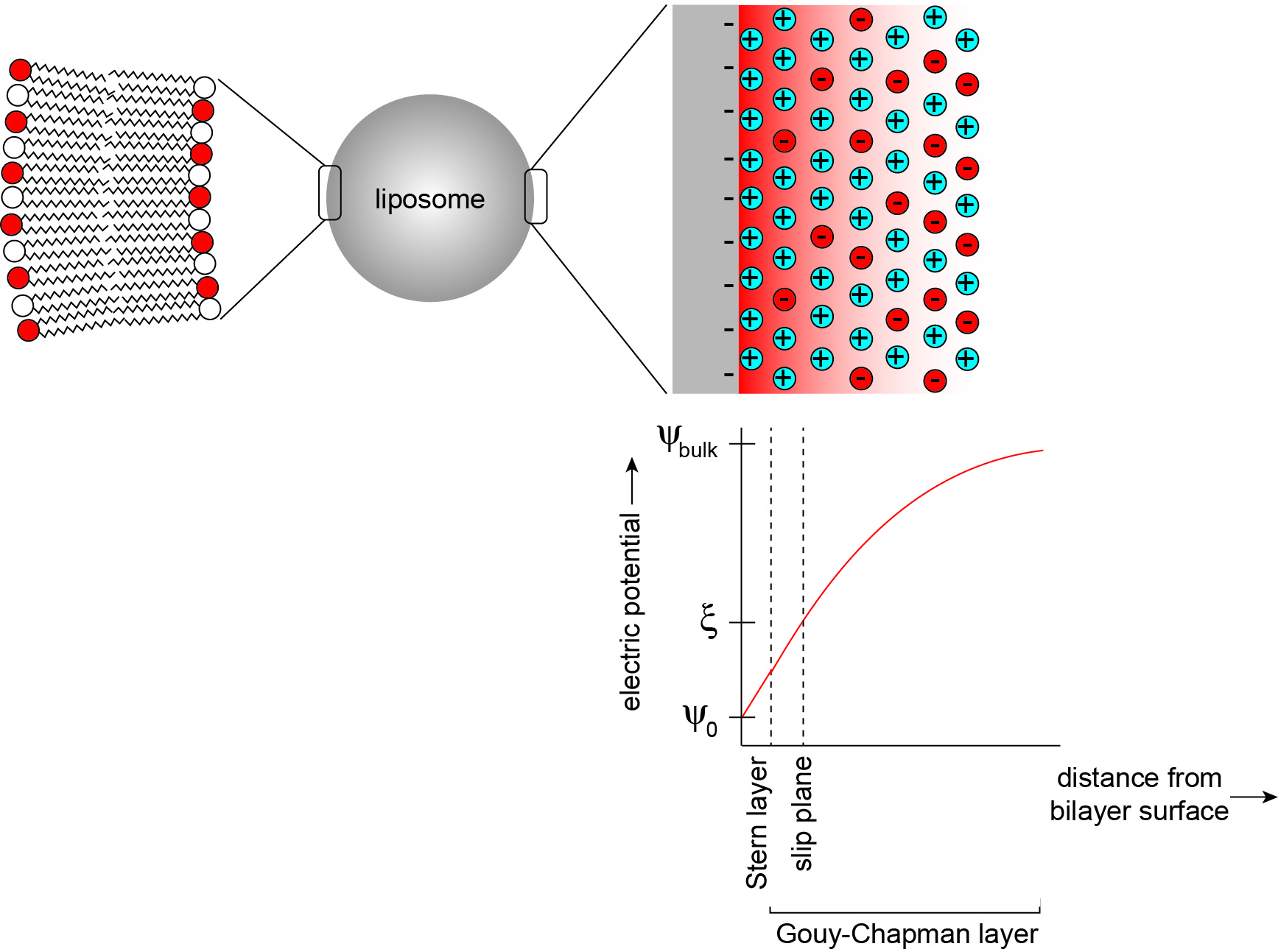
Figure 2. The electrostatic profile of the diffuse double layer. A liposome is a model membrane that consists of a vesicular lipid bilayer (left), whose surface and interfacial region in the aqueous phase can be modeled as an electrical double layer (right). In this model, a bilayer surface containing anionic phospholipids is modeled as a planar surface (gray) with uniformly distributed negative charges, from which an electric field originates (red shading). The distribution of solution electrolytes is shown for counterions (in this case, cations shown in blue) and coions (in this case, anions shown in red). Within the Stern layer, counterions are firmly bound to the bilayer surface. Within the Gouy-Chapman layer, solution ions are more disperse, reflecting a balance between Coulombic attraction (cations) or repulsion (anions) and thermal motion. The titratable charged lipid headgroups and adsorbed counterions together define the surface charge density (σ). The electric potential (ψ) assumes a maximum magnitude at the interface surface (ψ0) and attenuates toward the bulk solution (ψbulk) in a manner that is dependent on the ionic characteristics of the bathing solution. The electric potential at the slip plane, termed the zeta potential (ζ) is the measured parameter in this protocol.
Materials and Reagents
- Kimble Corex tubes (30 ml) (Thermo Fisher Scientific, Fisher Scientific, catalog number: 0950037 )
- Hamilton gas-tight syringe (Avanti Lipids Polar, catalog number: 610017 )
- Polycarbonate membrane filters, 0.4 µm (Avanti Lipids Polar, catalog number: 610007 )
- Wide-range pH test paper (Thermo Fisher Scientific, Fisher Scientific, catalog number: 14-850-1 )
- Glass tube
- 4 ml semi-micro cuvettes (SARSTEDT, catalog number: 67.745 )
- Hellma Suprasil quartz cuvette (Sigma-Aldrich, catalog number: Z802433 )
- Glass vials
- N2
- 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1’-rac-glycerol) (POPG) (Avanti Lipids Polar, catalog number: 840457C ) (Note 1)
- Chloroform (Thermo Fisher Scientific, Fisher Scientific, catalog number: C298 )
- Sodium chloride (NaCl) (Sigma-Aldrich, catalog number: S9888 )
- Teflon-lined closures (Avanti Lipids Polar, catalog number: 600460 )
- 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) (Avanti Lipids Polar, catalog number: 850457C )
- 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphethanolamine (POPE) (Avanti Lipids Polar, catalog number: 850757C )
- Ethanol
- Potassium chloride (KCl)
- Citric acid monohydrate (C6H8O7·H2O) (Sigma-Aldrich, catalog number: C1909 )
- Sodium phosphate dibasic (Na2HPO4) (Sigma-Aldrich, catalog number: S7907 )
- 2-amino-2-methyl-1,3-propanediol (AMPD) (Sigma-Aldrich, catalog number: A9754 )
- Iron (III) chloride hexahydrate (FeCl3·6H2O) (Sigma-Aldrich, catalog number: 236489 )
- Millipore filter sterilized water (ddH2O) (EMD Millipore, catalog number: Milli-Q Advantage A10 water purification system )
- Ammonium thiocyanate (NH4SCN) (Sigma-Aldrich, catalog number: 221988 )
- Citrate-phosphate buffers (see Recipes)
- AMPD buffer (see Recipes)
- Ammonium ferrothiocyanate solution (see Recipes)
Equipment
- Nitrogen tank
- Fume hood
- Vacuum desiccator (Eppendorf, model: Vacufuge Plus )
- Nanoparticle size analyzer (Malvern Instruments, model: Zetasizer Nano S90 ) (Zetasizer Nano Series Technical Note, Malvern Instruments: https://caliscc.org/images/presentations/Morante_Zeta_Potential.pdf)
- NanosphereTM polymer microsphere size standards, size 60 ± 2.7 nm (Thermo Fisher Scientific, Thermo ScientificTM, catalog number: 3060A )
- Pasteur pipette
- Vortexer (Bio-Rad Laboratories, model: BR 2000 )
- Filter supports (Avanti Lipids Polar, catalog number: 610014 )
- AccumetTM pH meter (Thermo Fisher Scientific, Fisher ScientificTM, catalog number: AB15 Plus )
- Avanti Mini Extruder Kit (Avanti Lipids Polar, catalog number: 610023 )
- Spectrophotometer (Thermo Fisher Scientific, Fisher Scientific, model: Ultrospec 2100 Pro )
- Zeta potential analyzer (Brookhaven Instruments, model: ZetaPlus Zeta Potential Analyzer )
- Zeta potential reference material (Brookhaven Instruments, catalog number: BI-ZR5 )
Software
- Zetasizer software
- Microsoft Excel
Procedure
- Liposome preparation
- Aliquot the desired lipid volumes into Kimble Corex tubes using a gas-tight syringe. For the illustrated protocol, add 200 μl of 25 mg/ml POPG chloroform stock into the tube. (Notes 2 and 3)
- The lipids are dried under a gentle N2 steam in a fume hood for approximately 30 min (Note 4).
- To remove residual chloroform, the lipids are further dried overnight under a vacuum in the desiccator.
- The dried lipids are hydrated and resuspended by vigorous vortexing in 1 ml of respective phosphate citrate buffer (pH 2.0 to 8.0) or AMPD buffer (pH 8.0 to 10.0) (see Recipes) and incubated for an additional 30 min (Note 5).
- The hydrated lipids are extruded each set 19 times through a 0.4 μm membrane maintained at proper temperature (Note 6).
- Aliquot the desired lipid volumes into Kimble Corex tubes using a gas-tight syringe. For the illustrated protocol, add 200 μl of 25 mg/ml POPG chloroform stock into the tube. (Notes 2 and 3)
- Quality control and liposome sizing
- The resulting liposomes are analyzed by dynamic light scattering in a Zetasizer Nano S90 to confirm the homogeneity and the accurate size of the samples prepared as shown in Figure 3A.
- Size measurements are performed using 90° scattering optics with the following measurement parameters. Temperature: 25 ± 1 °C; Dispersant: phosphate buffered saline; Refractive index: 1.332; Viscosity: 0.9128 cP; Equilibration time: 1 min; Measurement: automatic; Analysis model: general purpose (normal resolution). Instrument calibration is conducted using NanosphereTM size standards.
- 60 μl of each sample is placed in a quartz cuvette and measured with three successive runs at 1 min intervals.
- The scattering data are analyzed by Zetasizer software as shown in Figures 3B and 3C.
- Size measurements are performed using 90° scattering optics with the following measurement parameters. Temperature: 25 ± 1 °C; Dispersant: phosphate buffered saline; Refractive index: 1.332; Viscosity: 0.9128 cP; Equilibration time: 1 min; Measurement: automatic; Analysis model: general purpose (normal resolution). Instrument calibration is conducted using NanosphereTM size standards.
- The pH of the liposomes after extrusion is verified by using a pH paper as shown in Figure 3D.
- Measurement of the lipid concentration of vesicle samples is conducted using established colorimetric assay that measures the phospholipid-ammonium ferrothiocyanate complex (Marom and Abdussalam, 2013).
- Calibration curves are produced as follows:
- Add 40 μl POPG (25 mg/ml) to 9.96 ml of chloroform in a glass tube to prepare a stock solution of 0.1 mg/ml POPG.
- Make 11 samples of POPG in a glass tube as shown in Table 1.
- Vortex the samples for 1 min each after the addition of ammonium ferrothiocyanate and chloroform.
- Two separate phases will become evident. Using a Pasteur pipette, carefully remove the upper phase and discard it.
- Transfer the lower phase to a suitable cuvette and measure the absorbance at 488 nm using a spectrophotometer. The sample without POPG is used as blank.
- The graph of absorbance at 488 nm versus lipid concentration (mg/ml) serves as the calibration curve (Figure 3E).
Table 1. The reaction mixture for plotting the calibration curve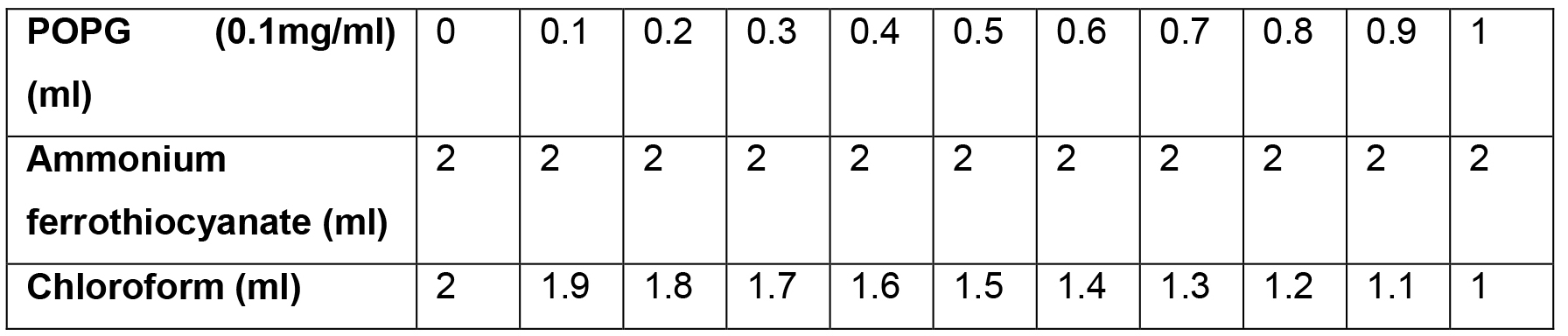
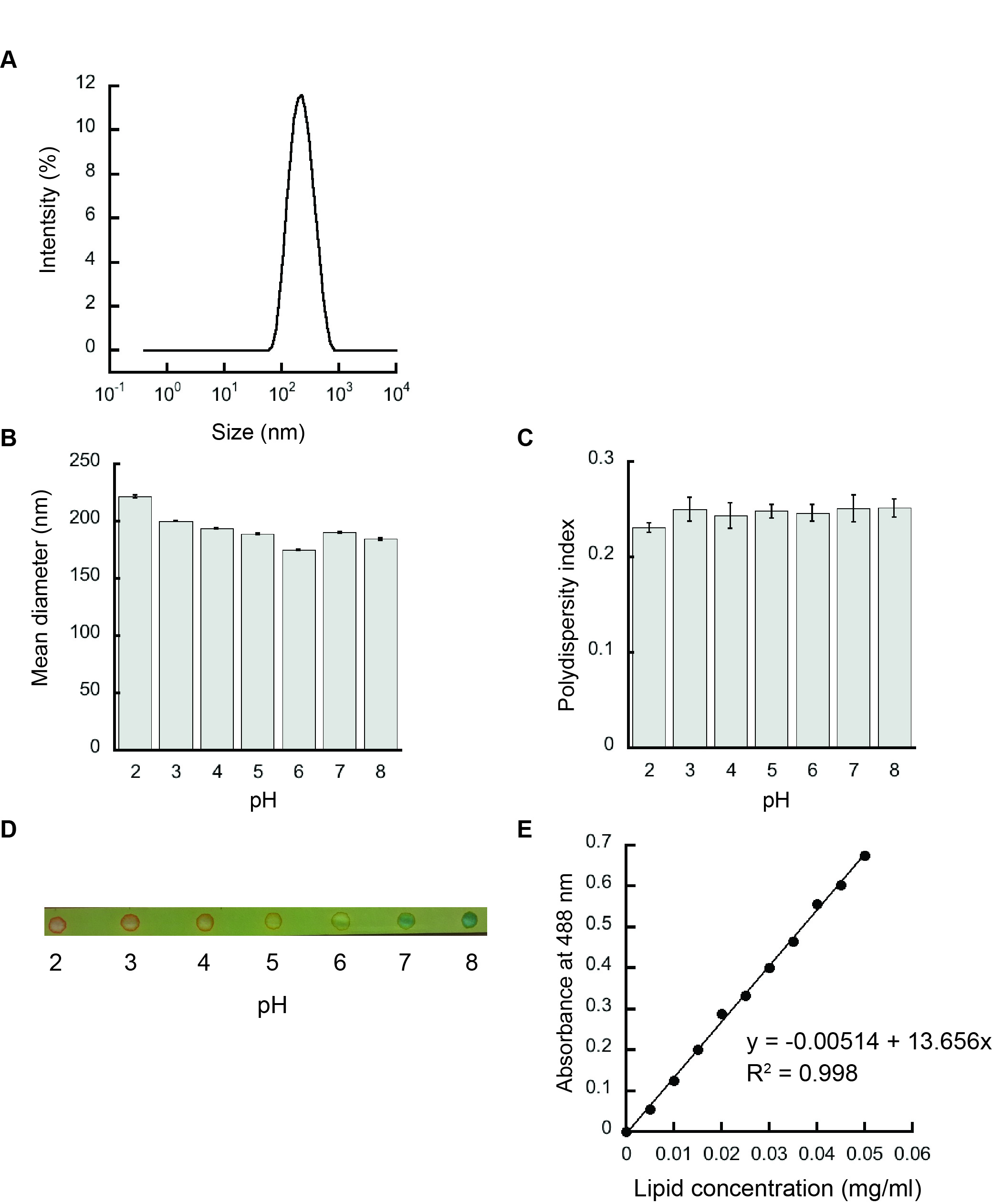
Figure 3. Liposome characterization. A. Representative intensity distribution trace for liposomes prepared from 100 mol% POPG by dynamic light scattering indicating a homogenous population. B. Mean diameters (Z-average values) of 100 mol% POPG liposomes. C. Polydispersity indices of 100 mol% POPG liposomes. D. The respective pH of liposomes after hydration and extrusion in various pH buffers verified using a pH paper. E. Representative phospholipid calibration curve.
- Add 40 μl POPG (25 mg/ml) to 9.96 ml of chloroform in a glass tube to prepare a stock solution of 0.1 mg/ml POPG.
- The lipid concentration of liposome samples is measured as follows:
- Add 10 μl of prepared liposomes into a glass tube. Add 2 ml ammonium ferrothiocyanate and vortex for 1 min.
- Add 1.99 ml of chloroform and vortex for 1 min.
- The lower phase is taken and the absorbance is measured at 488 nm.
- The respective lipid concentration is calculated by using the calibration curve, making sure to multiply the measured concentration by 200 to get the final concentration (1:200 dilution).
- Liposomes are diluted to a concentration of 1 mg/ml in the respective buffer.
- Add 10 μl of prepared liposomes into a glass tube. Add 2 ml ammonium ferrothiocyanate and vortex for 1 min.
- Calibration curves are produced as follows:
- The resulting liposomes are analyzed by dynamic light scattering in a Zetasizer Nano S90 to confirm the homogeneity and the accurate size of the samples prepared as shown in Figure 3A.
- Zeta potential measurements are conducted using a ZetaPlus Zeta Potential Analyzer (see Reference 10)
- Add 1.6 ml of 1 mg/ml liposomes sample in 4 ml-semi micro cuvettes.
- Open the ZetaPlus software and change the appropriate conditions in the ‘Parameters’ Dialogue box. The measurement parameters are as follows. Electric field: 14.86 V/cm; Current 21.37 mA; Conductance: 3936 μS; Viscosity: 0.890 cP; Refractive index: 1.330; Dielectric constant: 78.54; Temperature: 25 °C. The electrodes used are ZetaPlus, SR-516 type electrode (Note 7).
- The measurements are made for three runs with ten cycles (Note 8).
- Add 1.6 ml of 1 mg/ml liposomes sample in 4 ml-semi micro cuvettes.
Data analysis
The protocol presented above allows for the acquisition of zeta potential values for POPG-containing liposomes under a range of pH values. The goal of the data analysis is to evaluate the pKa value of the component lipids based on these data. In this section, we first give a brief overview of the theoretical and mathematical considerations involved in this analysis. We then present a stepwise process for thoroughly evaluating the data.
- Theory and modeling
- The electrostatic profile of the diffuse double layer perpendicular to the plane of the bilayer (Figure 2) is modeled using Gouy-Chapman-Stern formalism. In this concise theoretical overview, we present the relevant equations in this analysis; for further information on theory and mathematical derivation, the reader is referred to several background resources (McLaughlin, 1977; Oshima, 2010; Aveyard and Haydon, 1973) and to our recent publication (Sathappa and Alder, 2016) upon which this analysis is based.
- There are several simplifying assumptions of the Gouy-Chapman-Stern model, including: (i) that the membrane can be considered an infinite planar surface with bound charges uniformly smeared at x = 0; (ii) that the dielectric constant of the solution is constant at all x > 0; and (iii) that solution ions can be treated as point charges. In this model, the variable x represents the distance from the bilayer surface (see Figure 2).
- The bilayer surface charge originates from the titratable functional groups on the lipids and the adsorbed ions from solution. The maximal intrinsic surface charge from lipid groups (σmax j) is defined by the molar fraction-weighted maximal surface charge density of each lipid species j
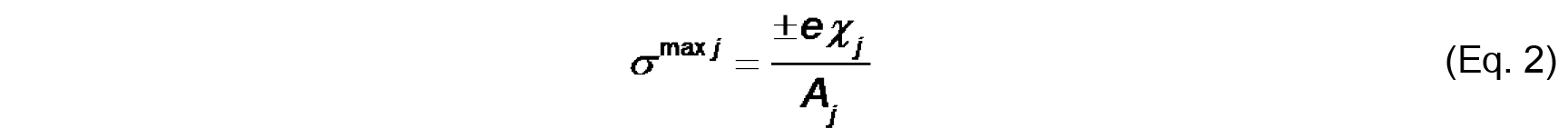
Where,
e is either the total formal charge or the elementary charge (± 1.6022 x 10-19 C) on the ionized titratable group,
χj is the molar fraction of species j,
Aj is the cross-sectional area of species j.
We assume for this analysis that Aj of a typical phospholipid is 70 Å2 and does not change with protonation state or complexation with ions. Note that σmax j is a constant for a given lipid system (Note 9). - The effective charge density of lipid headgroups (σ) under different conditions is modeled as a Langmuir adsorption isotherm that accounts for both the protonation state of the headgroup (depending on the surface pH) and on specific binding of solution counterions (depending on the surface concentration of ions). For the example given here, we need only account for the headgroup phosphate as the acidic ionizable headgroup charge and the presence of monovalent counterions; hence, the equation for σ takes the form:
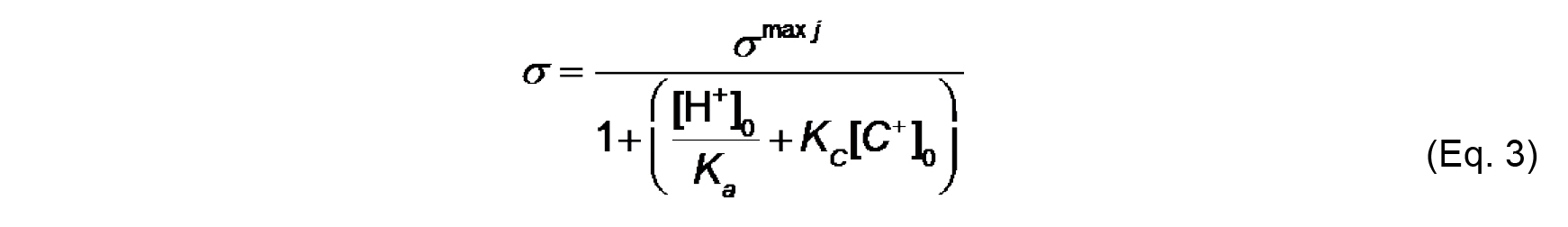
Where,
[H+]0 and [C+]0 are the surface concentrations of protons and monovalent cations, respectively (each in units of molarity, M),
Ka (M) is the acid dissociation (ionization) constant,
KC (M-1) is the association constant for 1:1 binding of the monovalent cation to the headgroup. The distribution of ions in the direction normal to the membrane surface is determined by Boltzmann statistics. Thus, the surface concentrations [H+]0 and [C+]0 can be defined from concentrations in the bulk, [H+]∞ and [C+]∞ as follows: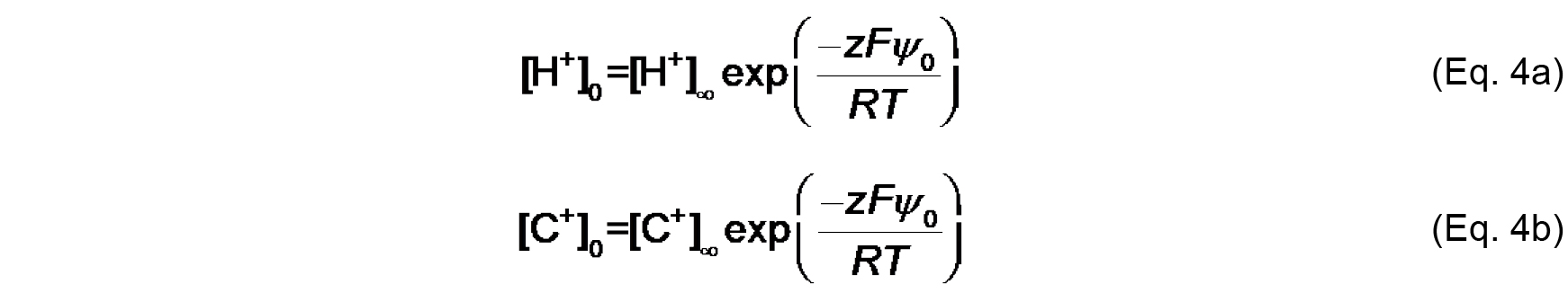
Where,
z is the valence of the relevant species,
F is the Faraday constant (9.649 x 104 C mol-1),
R is the universal gas constant (8.314 J mol-1 K-1),
T is the absolute temperature (K),
ψ0 (V) is the electric potential at the surface (relative to the bulk, ψ∞).
Note that the work (in J mol-1) required to bring an ion from infinity to a position with electric potential ψ is quantified as zF ψ. Therefore, based on the Boltzmann distribution, there will be an accumulation of protons and cations (z = +1) and a decrease in anions (z = -1) at distances approaching the negatively charged bilayer surface. - The Gouy-Chapman equation, based on the Poisson-Boltzmann relationship, relates surface potential (ψ0) and surface charge density (σ):
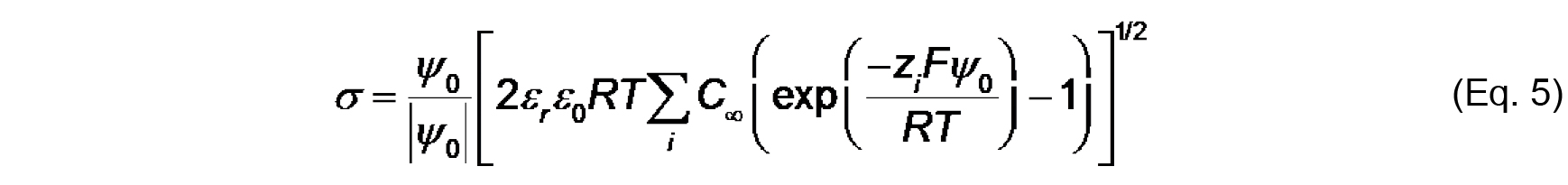
Where,
C is the bulk concentration of ion of valence z.
Values of ψ0, σ and Ka can be determined by the simultaneous evaluation of Eq. 3-5. - Finally, the electrostatic profile in the direction normal to the bilayer surface is used to determine σ0 from measurements of ζ (see Figure 2). To quantify ψ as a function of distance from the surface, we first consider the Debye constant, κ (m-1), quantified as
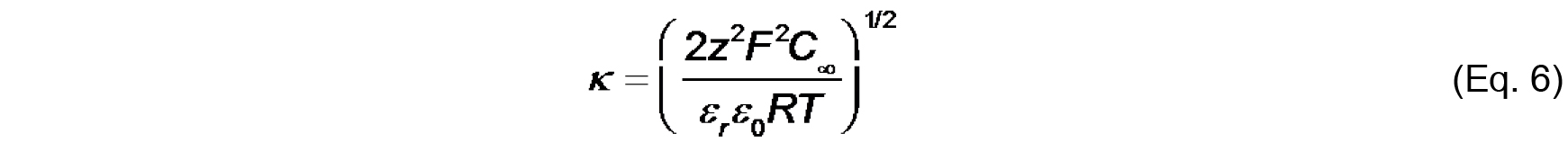
The value, κ-1 (m), is called the Debye length, which represents a measure of the thickness of the diffuse double layer. As shown in Eq. 6, the Debye length depends on the concentration and valence of electrolyte in the solution near the solid-aqueous interface. The higher the ionic strength (and higher valence of component ions), the more effectively solution ions will screen the electric field from the surface, thereby more rapidly attenuating the electric potential and reducing the extent of the double layer. - The distance-dependent decay of the electric potential from the membrane surface is quantified by the following relationship:
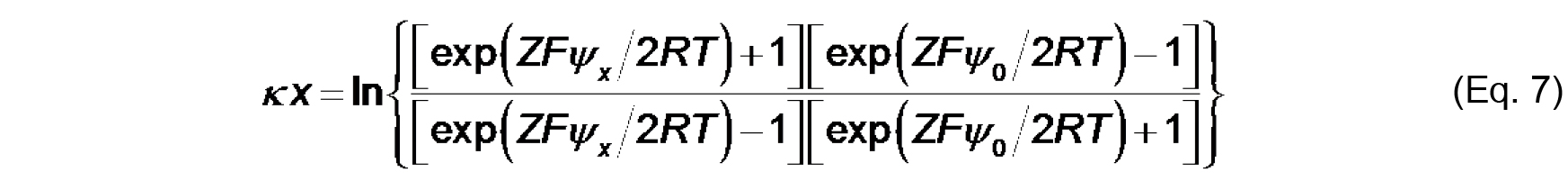
Where,
x (m) is the distance from the membrane plane,
ψx is the electric potential at that distance. To calculate ψ0 from measurements of ζ based on these relationships, we must make an assumption about the distance at which the shear plane exists such that for each measured value of zeta potential, we can assume that ζ = ψx.
- The electrostatic profile of the diffuse double layer perpendicular to the plane of the bilayer (Figure 2) is modeled using Gouy-Chapman-Stern formalism. In this concise theoretical overview, we present the relevant equations in this analysis; for further information on theory and mathematical derivation, the reader is referred to several background resources (McLaughlin, 1977; Oshima, 2010; Aveyard and Haydon, 1973) and to our recent publication (Sathappa and Alder, 2016) upon which this analysis is based.
- Data analysis
In the presented methodology, ζ measurements over a range of solution pH values are analyzed to evaluate the pKa of the component lipid. The quantitative analysis described here is delineated into three steps, each one described below with reference to the theoretical considerations from the previous section. In our previous work (Sathappa and Alder, 2016), we primarily used Wolfram Mathematica 10 for quantitative evaluation. But for the present analysis, we have adapted this as a more simplified approach for use with Microsoft Excel. A representative Excel worksheet is presented in Figure 4, which explicitly shows all three stages of analysis along with the way in which each cell should be populated. The spreadsheet represents a mock data set in which POPG liposomes were subjected to zeta potential measurements in the presence of 10 mM monovalent electrolyte over a range of pH values (pH 1-9) (Note 10). The input values of ζ in this example are as follows:
pH 1, ζ = -6.899 mV; pH 2, ζ = -27.273 mV; pH 3, ζ = -57.717 mV
pH 4, ζ = -88.171 mV; pH 5, ζ = -110.527 mV; pH 6, ζ = -118.836 mV
pH 7, ζ = -120.118 mV; pH 8, ζ = -120.255 mV; pH 9, ζ = -120.268 mV- Step 1: Enter experiment parameters
- The first column relates to characteristics of the model lipid system:
- Cell C4 (data input): This is the formal charge per ionized lipid headgroup. POPG is an anionic lipid with a maximum of one negative charge per lipid; therefore, a value of -1 is input here.
- Cell C5 (data input): This is the mol% anionic lipid in the model system. In this example, liposomes are pure POPG (χPOPG = 1.0); therefore, a value of 100 is entered here.
- Cell C6 (formula input): This calculation of surface charge density is a form of Eq. 2 that quantifies σ in terms of total charge per Å2.
- Cell C7 (formula input): This recasts σ in terms of C m-2 for use in the adsorption isotherm for direct comparison with the Gouy-Chapman equation.
- Cell C4 (data input): This is the formal charge per ionized lipid headgroup. POPG is an anionic lipid with a maximum of one negative charge per lipid; therefore, a value of -1 is input here.
- The second column relates to the ionic characteristics of the bathing solution:
- Cell H3 (data input): This is the molar concentration of monovalent electrolyte in the solution. In this example, the solution contains 10 mM NaCl; therefore, a value of 0.01 is entered here.
- Cell H4 (formula input): This is the formula input for the Debye constant κ (Eq. 6), given that |z| = 1 and assuming that εr = 80 and T = 298K.
- Cell H5 (formula input): This is the calculated value of the Debye length, 1/κ, in terms of m.
- Cell H6 (formula input): This recasts 1/κ in terms of Å.
- Cell H7 (data input): This is the assumed distance x of the slip plane from the surface of the bilayer (correlating with the point at which ψx = ζ). Based on previous work [Sathappa and Alder (2016) and references therein], a value of 2 Å should be input here.
- Cell H8 (formula input): This is the product of κ and x, which is used in Eq. 7.
- Cell H3 (data input): This is the molar concentration of monovalent electrolyte in the solution. In this example, the solution contains 10 mM NaCl; therefore, a value of 0.01 is entered here.
- The first column relates to characteristics of the model lipid system:
- Step 2: Calculate surface potential
- For each pH-specific value of ζ, the corresponding value of ψ0 is calculated.
- Cells A13-A21 (data input): The values of bulk pH for each reading.
- Cells B13-B21 (formula input): This converts bulk pH to bulk [H+] in units of molarity.
- Cells C13-C21 (data input): The values of ζ (V) for each pH condition are entered.
- Cells D13-D21 (formula input): This is a rearrangement of Eq. 7 that is used as the objective cell in the Solver protocol to calculate ψ0.
- Cells E13-E21 (calculated values): These are the variable cells in the Solver protocol. For consistency, set each cell equal to -0.00001 prior to running Solver.
- Cells A13-A21 (data input): The values of bulk pH for each reading.
- To calculate ψ0 for each given ζ using Solver, open Solver (from the Excel ‘Tools’ dropdown menu) and perform the following for each data point:
- Set objective for the relevant ‘Eq. 7’ cell (e.g., D13 for the ‘pH 1’ point) to a value of 0.
- Assign the variable cell as the relevant ‘ψ0 (V)’ cell (e.g., E13 for the ‘pH 1’ point).
- Make sure that unconstrained variables can be negative.
- Click Solve
- Set objective for the relevant ‘Eq. 7’ cell (e.g., D13 for the ‘pH 1’ point) to a value of 0.
- For each pH-specific value of ζ, the corresponding value of ψ0 is calculated.
- Step 3: Calculate surface charge density and pKa
- First, the Gouy-Chapman equation (Eq. 5) is used to calculate the effective surface charge density. Second, this value is equated with the adsorption isotherm (Eq. 3) to solve for the measurement-specific Ka value.
- Cells G13-G21 (formula input): This is the Gouy-Chapman equation, which calculates σ based on the known concentration of electrolytes in solution and the calculated values of ψ0.
- Cells H13-H21 (formula input): This is the calculation of the surface H+ concentration based on the Boltzmann distribution (Eq. 4a).
- Cells I13-I21 (formula input): This is the calculation of the surface cation concentration based on the Boltzmann distribution (Eq. 4b).
- Cells J13-J21 (formula input): This is an algebraic manipulation of Eq. 3, which solves for Ka assuming that the association constant of cation adsorption to the POPG headgroup is 0.6 M-1.
- Cell J22 (formula input): This takes the average Ka value for all measurements and converts it to a pKa value.
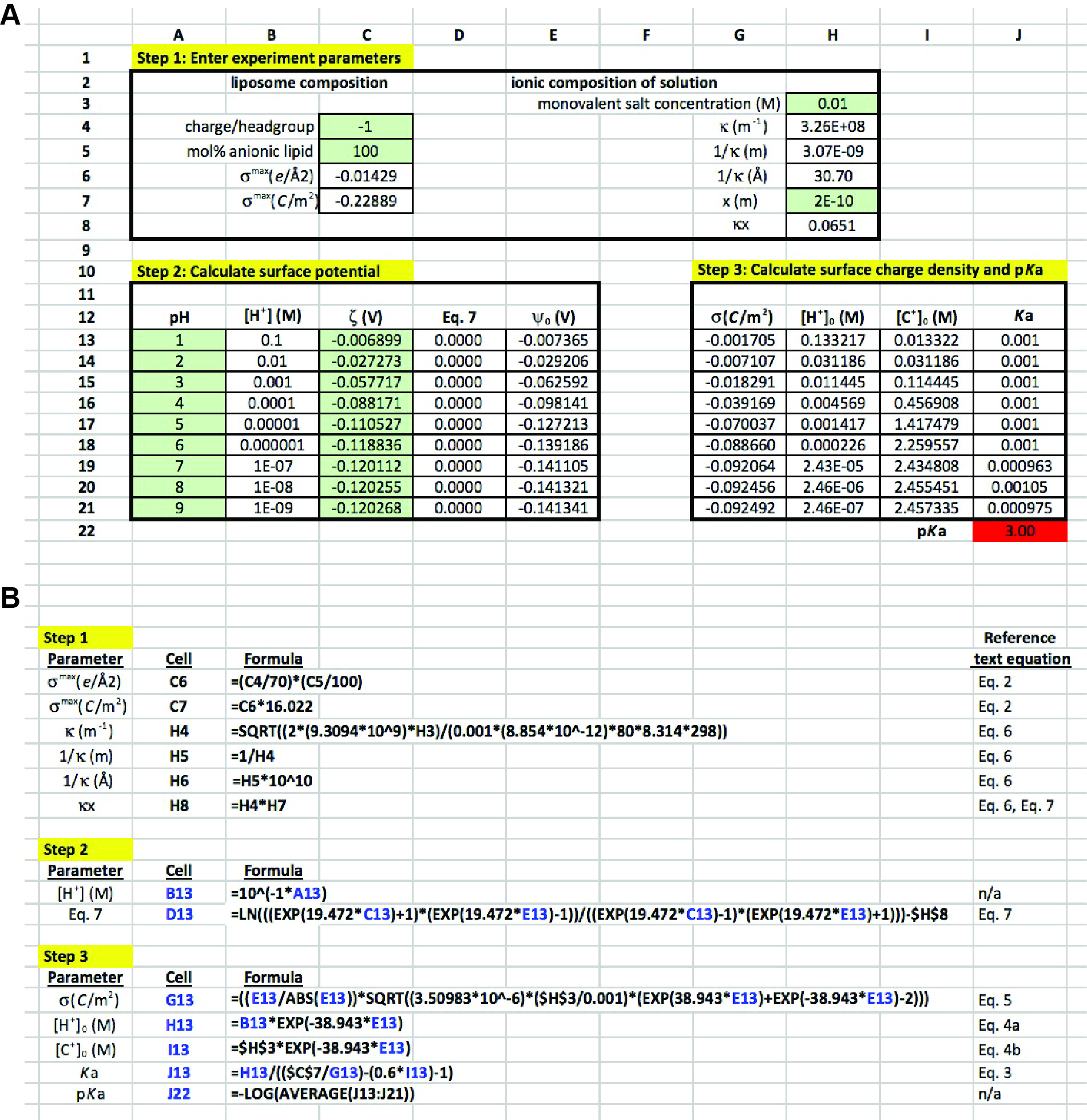
Figure 4. Excel sheet workup for data analysis. A. Data entry cells, subdivided into steps 1-3. Cells in green are those used for direct data input. Non-shaded cells are those either containing formulas or calculated values. See text for detailed explanation. B. Input for formula cells, along with corresponding equations from the text. Cells and variables highlighted in blue are those that are copied from rows 13 to 21 within each column.
- Cells G13-G21 (formula input): This is the Gouy-Chapman equation, which calculates σ based on the known concentration of electrolytes in solution and the calculated values of ψ0.
- First, the Gouy-Chapman equation (Eq. 5) is used to calculate the effective surface charge density. Second, this value is equated with the adsorption isotherm (Eq. 3) to solve for the measurement-specific Ka value.
- Step 1: Enter experiment parameters
Notes
- All lipid stocks in chloroform should be stored in glass vials with Teflon-lined closures at -20 °C.
- The lipid stocks are thawed to room temperature under a fume hood for 15 min before aliquoting into Kimble Corex tubes. It is essential that plastic does not come into contact with lipid stocks in chloroform, as this solvent will leach impurities from the plastic. Hamilton gas-tight syringes should be used to transfer lipid stocks in organic solvents.
- It is also possible to prepare liposomes with a heterogeneous composition of synthetic lipids by preparing a blend of lipids at this stage. For example, the phospholipids 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC); 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE); and POPG can be used to prepare liposomes composed of POPC:POPE:POPG (40:40:20 mol%) by mixing 85 μl of 25 mg/ml POPC, 81 μl of 25 mg/ml POPE and 43 μl of 25 mg/ml POPG prior to drying down the lipids.
- Lipid drying times under the nitrogen stream will vary. In general, once the first white residue begins to appear, drying is continued for an additional 10-15 min. When dried, the lipids will develop a thin film at the bottom of the glass tube. Avoid excessive drying, as this will make hydration and resuspension of the lipid film difficult.
- Make sure the temperature of the hydration buffer and extruder are above the phase transition temperature (Tm) of the lipid being used (or the Tm of the lowest-melting lipid in a heterogeneous blend). If the target Tm is above room temperature, all buffers should be brought above the Tm in a temperature-controlled incubator and the extruder heating block assembly should be equilibrated to the desired temperature atop an adjustable hot plate prior to extrusion. Note that the Tm of POPG is -2 °C; therefore, the illustrated protocol can be carried out at room temperature.
- The extruder is assembled in accordance with manufacturer’s instructions (https://avantilipids.com/tech-support/liposome-preparation/luvet/). To reduce the dead volume during extrusion, pre-wet all extruder parts by passing the appropriate buffer through the assembled extruder, then discarding the buffer. The final extrusion should be taken from the opposite syringe used to load the sample to reduce contamination. During extrusion, lipid samples generally go from being hazy to more transparent. Between sample preparations, wash the extrusion parts thoroughly with water, ethanol, then allow to air dry to reduce contamination.
- The instrument parameters must be modified in accordance with the buffer, pH and temperature of each run. Instrument calibration is conducted using BI-ZR5 zeta potential reference material in 1 mM KCl at -49 mV ± 4 mV.
- After each run, the liposomes in the cuvettes should be mixed well, to avoid settling of liposomes to the bottom of the cuvette.
- For information on modeling multicomponent systems containing different lipids with differing pKa values, refer to our recent publication (Sathappa and Alder, 2016).
- In practice, a smaller pH range will be required to maintain stability of the liposome samples. The wide pH range (1-9) given in this theoretical example is for illustrative purposes only to allow the reader to understand the conceptual basis of the analysis.
Recipes
- Citrate-phosphate buffers (100 ml each, pH 2-8, each with 10 mM NaCl)
- Prepare 0.1 M solution of citric acid solution by dissolving 0.58 g NaCl and 21.01 g of citric acid monohydrate in 1 L of ddH2O.
- Prepare 0.2 M solution of phosphate solution by dissolving 0.58 g NaCl and 28.40 g of dibasic sodium phosphate in 1 L of ddH2O.
- Mix citric acid and phosphate at the following volumes to obtain buffered solutions of the following pH values (Table 2):
Table 2. Phosphate citrate buffer recipe
- Prepare 0.1 M solution of citric acid solution by dissolving 0.58 g NaCl and 21.01 g of citric acid monohydrate in 1 L of ddH2O.
- AMPD buffer (100 ml, each with 10 mM NaCl)
- Prepare 0.2 M solution of AMPD by dissolving 0.058 g NaCl and 21.03 g of AMPD in 90 ml of ddH2O.
- Set solution to desired pH using 6 N NaOH (initial pH will be approximately 7.6).
- Adjust final volume to 100 ml with ddH2O.
- Prepare 0.2 M solution of AMPD by dissolving 0.058 g NaCl and 21.03 g of AMPD in 90 ml of ddH2O.
- Ammonium ferrothiocyanate solution
Dissolve 27.3 g FeCl3·6H2O and 30.4 g ammonium thiocyanate in 1 L ddH2O.
Acknowledgments
This protocol was adapted from our recent published work (Sathappa and Alder, 2016). Research in the Alder Group is supported by National Institutes of Health Grant 1R01GM113092, National Science Foundation Grant MCB-1330693, and a Barth Syndrome Foundation Research Grant (to N.N.A.).
References
- Aveyard, R. and Haydon, D. A. (1973). An introduction of the principles of surface chemistry. Cambridge University Press.
- Delgado, A. V., Gonzalez-Caballero, F., Hunter, R. J., Koopal, L. K., Lyklema, J., International Union of, P., Applied Chemistry, P. and Biophysical Chemistry Division, I. T. R. (2007). Measurement and interpretation of electrokinetic phenomena. J Colloid Interface Sci 309(2): 194-224.
- Gennis, R. B. (1989). Biomembranes molecular structure and function. Springer.
- Marom, M. and Abdussalam, A. (2013). The use of cardiolipin-containing liposomes as a model system to study the interaction between proteins and the inner mitochondrial membrane. Methods Mol Biol 1033: 147-155.
- Marsh, D. (2013). Handbook of lipid bilayers, Second Edition. CRC Press.
- McLaughlin, S. (1977). Electrostatic potentials at membrane-solution interfaces. Curr Top Membr Transp 9: 71-144.
- Oshima, H. (2010). Biophysical chemistry of biointerfaces. Wiley.
- Sathappa, M. and Alder, N. N. (2016). The ionization properties of cardiolipin and its variants in model bilayers. Biochim Biophys Acta 1858(6): 1362-1372.
- Tocanne, J. F. and Teissie, J. (1990). Ionization of phospholipids and phospholipid-supported interfacial lateral diffusion of protons in membrane model systems. Biochim Biophys Acta 1031(1): 111-142.
Article Information
Copyright
© 2016 The Authors; exclusive licensee Bio-protocol LLC.
How to cite
Sathappa, M. and Alder, N. N. (2016). Ionization Properties of Phospholipids Determined by Zeta Potential Measurements. Bio-protocol 6(22): e2030. DOI: 10.21769/BioProtoc.2030.
Category
Biochemistry > Lipid > Lipid measurement
Do you have any questions about this protocol?
Post your question to gather feedback from the community. We will also invite the authors of this article to respond.
Share
Bluesky
X
Copy link