Numerical methods

We modeled the long-term dynamics and diversity of ecological communities using the well-known generalized Lotka-Volterra (gLV) model, modified to include dispersal from a species pool:

where N_i is the abundance of species i (normalized to its carrying capacity), α_ij is the interaction strength that captures how strongly species j inhibits the growth of species i (with self-regulation α_ii = 1), and D is the dispersal rate from an outside species pool to the focal community. For simplicity and without qualitatively changing our results, we considered the same growth rate 

 = 1 and the same carrying capacity 

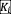
= 1 for all species in the main text. Fig. S6 shows that sampling growth rates from a uniform distribution has little effect on the phase diagram of survival fraction and fluctuation fraction. Fig. S6 shows that sampling carrying capacities from a normal distribution increases the partial coexistence phase while shrinking both the full coexistence phase and fluctuation phase, but does not affect the order of the phases. We further tested the theoretical predictions when considering the existence of positive (facilitative) interspecies interactions (Fig. S9) and varying the symmetry of the interaction matrix (Fig. S8). We also considered different dispersal rates (Fig. S7), and the effects of incorporating daily dilutions (Fig. S9) in these in silico communities. These additional results show that our qualitative phase diagrams and conclusions are robust to different choices of ecological network structure and parameters. Although the patterns of ecological diversity and dynamics do not change as the dispersal rate varies from D=10^-7 to D=10^-6 (Fig. S7), we found that communities with zero dispersal rate exhibit lower fluctuation fraction and survival faction in the persistent fluctuation phase. Our results show that non-zero dispersal rates can sustain persistent fluctuations.

To show that symmetry and anti-symmetry do not qualitatively change the phase diagram, we simulated communities in two scenarios of non-zero reciprocity, 

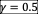
 and 

 , where the reciprocity of interactions is given by 

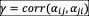
. The qualitative patterns and order of transitions in the phase diagram (Fig. S8) are robust to the presence of reciprocity, although 

 shifts the stability boundary (solid line in Fig. S8).  Positive and negative reciprocity decreases and increases the values of S and <

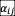
> at which communities lose stability, respectively. Moreover, positive (negative) reciprocity yields lower (higher) survival fraction and fluctuation fraction of communities. At full symmetry and anti-symmetry (

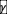
 =1, -1) there is no fluctuating phase (21), but those do not appear to be relevant from the experiment pair-competition results (Table. S1-S3). 

To test whether the existence of positive (facilitative) interactions in the ecological network will change our conclusions, we sampled values of 

 from a uniform distribution [-

, 

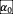
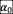
], where 

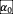
 varies between [0, 1.4] on the phase diagram. In this simulation, the linear interaction function in the gLV (

) is replaced with Monod function (

) to avoid unbounded growth due to positive interactions (21, 42). We observed similar patterns of survival fraction and fluctuation fraction between pure competitive interactions and considering positive interactions (Fig. S9). The first and second moment of the distribution of 

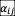
 should be considered to quantify interaction strength in the stability criteria (17). Here we use Std (

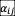
) to quantify the interaction strength because the first moment of 

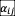
 distribution is zero. Our results demonstrate that the existence of three phases (full coexistence, partial coexistence, persistence fluctuation) and the order of transitions are robust to the interaction types in the model.

All simulations used the Runge-Kutta method on Matlab to numerically solve the LV equations (with an integration step of 0.05). A definition of 100 

100 pixels was used for each phase diagram, linearly segmenting the parameter space in the ranges <α_ij> ∈ [0, 1.5] and S ∈ [1, 100]. In each phase diagram, each pixel shows the average result for 10³ simulations. The total simulation time is 10⁴ to guarantee the survival fraction and fluctuation fraction have reached steady states as shown in Fig. S5. 

To test whether the total biomass fluctuation is consistent with species abundance fluctuation in our simulations, we simulated the time series of community biomass under various conditions (Fig. S3). To quantify the dynamics of biomass in the simulation, we calculated the sum of species abundance (

). Our results demonstrate the fluctuation in species abundance is in agreement with fluctuation in total biomass.

The similar fluctuations between replicates in some experiments (e.g., Fig. 2, medium nutrients, S=48) could be explained by the slow divergence that chaotic trajectories can exhibit during moderately long-time windows, or, alternatively, by possible limit cycle oscillations (Fig. S3). We focused on chaotic fluctuations when discussing the model predictions because previous theory shows that all persistent fluctuations will be chaotic as number of species in the pool S grows (21), though limit cycle oscillations only happen under finite S.

Below are the Matlab code:

clear;clc;close all;
r_mean=1.0; % mean growth rate
S=1:1:100; % number of species 
DD=1e-6; % migration rate
A_mean_range=[0.01 1.5]; % mean inhibition alpha
ystep=100; %for A_mean
T_real=10000; %total evolution time
step=0.05; % time interval 
T=ceil(T_real/step); %number of circulation
num_sim=10000; % number of simulation
period=2000; % duration for calculating richness
% composition_full=zeros(length(S)*ystep*num_sim,length(S)); % record the final compositions of all simulations
abundance_threshold=1e-3; %threshold for survival species

fluc_record=zeros(length(S)*ystep,num_sim);
diversity_record=zeros(length(S)*ystep,num_sim); 
A_mean=linspace(A_mean_range(1),A_mean_range(2),ystep);

for mm=1:length(S)
   for pp=1:ystep
     for hh=1:num_sim
        composition= LV_compute(r_mean, S(mm), DD, A_mean(pp),T,step);  
        diversity_index=max(composition(T-period+1:T,:)); richness=find(diversity_index>abundance_threshold);
        diversity_record((mm-1)*ystep+pp,hh)=length(richness)/S(mm);
        fluc_CV=std(composition(T-1e5:T,:))./mean(composition(T-1e5:T,:)); fluc_CV(isnan(fluc_CV))=0;
        fluc_record((mm-1)*ystep+pp,hh)=mean(fluc_CV(fluc_CV>0));
     end
   end  
end

function [composition] = LV_compute(r_mean, S, D, A, T, step)

N_mean=1/(S*A*sqrt(pi/2)); 
sigma3=N_mean/12;
NN=zeros(T,S); 
r=ones(S,1);

% Interaction matrix
%   AA=exprnd(A,S,S);
   AA=rand(S,S)*A*2;
   AA=AA-diag(diag(AA))+eye(S);

% considering carrying capacity   
%  K=normrnd(1,sqrt(1/12),[S,1]);
%  for i=1:S
%      for j=1:S
%      AA(i,j)=AA(i,j)*K(j)/K(i);
%      end
%  end

% Initial composition
 N0=abs(normrnd(N_mean,sigma3,1,S)); 
 NN(1,:)=N0;

% Migration from source
  Migra=ones(1,S)*D;

% compute the dynamics in each patch
for i=2:T
      
      for j=1:S
          k1=r(j)*NN(i-1,j)*(1-AA(j,:)*(NN(i-1,:)'))*step;
          k2=r(j)*(NN(i-1,j)+k1/2)*(1-AA(j,:)*(NN(i-1,:)'))*step;
          k3=r(j)*(NN(i-1,j)+k2/2)*(1-AA(j,:)*(NN(i-1,:)'))*step;
          k4=r(j)*(NN(i-1,j)+k3)*(1-AA(j,:)*(NN(i-1,:)'))*step;
        NN(i,j)=NN(i-1,j)+(1/6)*(k1+2*k2+2*k3+k4);
     
      end

        NN(i,:)=NN(i,:)+Migra;
        
end

composition=NN;

end

clear; clc; close all;

load ./uniform3.mat;

load feasible_exp.mat

x_step=length(S); y_step=length(A_mean); 

miu1=A_mean(1); miu2=A_mean(length(A_mean)); S1=S(1); S2=S(length(S));

color12=[0.7 0.7 0.7];

 phase_indicate=mean(diversity_record,2); fluc_digi=fluc_record;

 phasenew_indicate=zeros(length(phase_indicate),1);

 critical_CV=0.001;

 for i=1:length(phasenew_indicate)

     for j=1:num_sim

     if fluc_record(i,j)<critical_CV

            fluc_digi(i,j)=0;

     else

         fluc_digi(i,j)=1;

     end

     end

 end

 fluc_indicate=mean(fluc_digi,2);

 phase_std=std(diversity_record,0,2)./phase_indicate;

 phasecolor=reshape(phase_indicate,[y_step,x_step]); phasecolor_std=reshape(phase_std,[y_step,x_step]); 

 phasecolor_fluc=reshape(fluc_indicate,[y_step,x_step]); phasecolor_new=reshape(phasenew_indicate,[y_step,x_step]);

 phasecolor_new1=zeros(y_step,x_step);

 x2=linspace(miu1,miu2,y_step)'; x1=sqrt(linspace(S1,S2,x_step))';  x2(1)=0;

 X1=repmat(x1',y_step,1); X2=repmat(x2,1,x_step); 

figure(1)

s=pcolor(X1.^2,X2,phasecolor);set(s, 'LineStyle','none'); colorbar; hold on;

   caxis([0.0 1.1])

   plot(xx3,yy3,'k-','linewidth',5,'color',color12)

    plot(ss,fea,'k-.','linewidth',5,'color',color12);

axis([S1 S2 0 1.5]); set(gca,'FontSize',28);

xlabel('Size of species pool, {\itS}','FontSize',30); ylabel('Interaction strength, <\it\alpha_i_j>','FontSize',30);

xticks([1 20 40 60 80 100]); yticks([0.0 0.5 1.0 1.5]); box on

figure(2)

p=0.9; 

sp=csaps({x1.^2,x2},phasecolor_fluc,p);

v=fnval(sp,{x1.^2,x2});

s=pcolor(X1.^2,X2,v);set(s, 'LineStyle','none'); colorbar; hold on;

   caxis([0.0 1])

   plot(xx3,yy3,'k-','linewidth',5,'color',color12)

   plot(ss,fea,'k-.','linewidth',5,'color',color12);

axis([S1 S2 0 1.5]); set(gca,'FontSize',28);

xlabel('Size of species pool, {\itS}','FontSize',30); ylabel('Interaction strength, <\it\alpha_i_j>','FontSize',30);

xticks([1 20 40 60 80 100]); yticks([0.0 0.5 1.0 1.5]); box on