Theoretical alternatives to the Lotka-Volterra model

Theoretical alternatives to the Lotka-Volterra model

The Lotka-Volterra model provides a phenomenological representation of bacterial growth and interactions, but our conclusions are not tied to this specific model. It is important to understand whether our central theoretical predictions generalize: how broadly do we expect a similar qualitative map of dynamical phases, where extinctions start to occur before the onset of fluctuations (as we increase either species pool size or interaction strength)? This empirically-observed ordering of phases is not self-evident: it is straightforward to construct few-species models that display fluctuations without extinctions, e.g. predator-prey pairs. Therefore, if our qualitative phase ordering appears across a range of many-species models and experiments, we may be seeing a broad mechanism, one that is presumably collective rather than driven by particular species. 

One interesting question is whether these collective dynamics emerge from many independent pairwise species interactions (as in our random Lotka-Volterra model), or whether they are driven by one or a few system-wide factors, such as public goods impacting all species. Ratzke et al. (14) performed bacterial experiments and introduced a different model where all interactions are mediated by modifications of the environmental pH by the bacteria, whose growth is in turn modified by pH.  This pH-based model, and a variant, reproduced some experimental results in (14, 33). We slightly amend the model in (14) to represent continuous-time dilution and dispersal from the species pool (we have also simulated discrete daily dilutions and dispersal, with no impact on our conclusions).

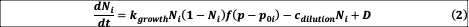
where 

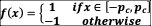
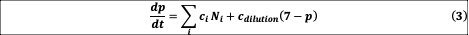
Equation (2) represents the growth of bacterial abundance 

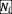
, which follows a logistic equation with parameter 

 modulated by the pH value 

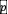
 : growth is maximal when this value is equal to species i’s pH optimum 

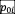
, (drawn uniformly over [4.5,9.5]), with a tolerance given by 

. In addition, parameter 

 (continuous-time equivalent to our 1:30 daily dilution) encompasses losses due to dilution, whereas 

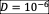
 represents dispersal from the species pool. Equation (3) represents the change of pH induced by the bacteria, and the return toward the neutral pH value of 7 due to dilution The distribution of 

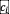
, drawn uniformly over [-c, c], thus determines the impact of bacteria on pH, and indirectly, the strength of interactions between bacteria.

We find that this model reproduces some of the main predictions of the Lotka-Volterra model: as seen in Fig. S10, the phase diagram with its three phases is qualitatively preserved in this second model, which suggests that it is highly robust to variations in modelling assumptions. Nevertheless, we believe that the LV model better reproduces our experimental results, whereas the pH-based model was more adequate in (14, 33), plausibly due to different taxa (species that exhibit ecological suicide do not appear in our species pool here) and experimental conditions (lower dilution rate) that lead to stronger impacts of pH.  Indeed, there are three points that make the LV model more plausible here:

1) In our experiments, pH fluctuations are only moderately correlated (Pearson correlation coefficient: 0.54) with fluctuations in optical density or species composition (whereas the latter two are highly correlated), suggesting that pH is not the sole driving factor of stability here. (Fig S11A)

2) The pH-based models in (14, 33) notably aimed to allow for ecological suicide, i.e. species growing then going extinctin monoculture, which does not occur in our experiment (In our initial species pool, we only retained species that survived in all of our growth conditions for the convenience of daily dispersal, Fig. S26). In the high-interaction strength regime and large initial species pool size regime, the pH-based model has two main outcomes: either many-species fluctuations, or total or near-total extinction with zero or few species surviving, and total biomass < 5% of carrying capacity (Fig S11B). Only the former behavior is seen in our experiments; the latter prediction of pH-based model was never observed in our experiments (Fig. 2C and Fig. S26).

3) The LV model displays positive correlation between the number of surviving species and the intensity of fluctuations, as in our experiments (Fig. 4 and Fig. S11), whereas the pH-based model displays a negative correlation (we excludecommunities falling under the above extinction criterion, which were never observed in our experiment, Fig. S11C). The positive relation between diversity and fluctuations, validated in our experiments, is key to our theoretical argument.

These three reasons lead us to retain the Lotka-Volterra model as our prime example (see Fig. S12 for a best-fit illustration). This cannot rule out a different pH-based model, or a combination of pH-based and direct interactions, as a good description of the biological mechanisms at play in our experimental setting.

We reach two main conclusions:

i) The random Lotka-Volterra model provides a straightforward prototype of a mechanism that fits our theoretical argument. The dynamical phases are unambiguously emergent, in the sense of being driven by species diversity and local pairwise interactions. The picture is as follows: the fluctuating phase must appear after extinctions and turnover in species composition, since fluctuations are driven by a tendency to jump between alternate sets of surviving species, each of themunstable. 

ii) We expect this central prediction to hold broadly under different modelling choices. Indeed, we find that the pH-based model displays an analogous set of regimes and transitions (Fig. S10), even though its predictions do not match some of our experimental results as accurately as the LV model (Fig. S11).

In both models, increasing the number of species and the strength of their interactions, whether direct or mediated through an abiotic factor, will typically lead to extinctions before it leads to loss of stability. This results in a phase of partial coexistence preceding a phase of instability, no matter whether species diversity and extinctions are necessary (as in the random LV model) or not (as in the pH-based model) for the mechanism that drives fluctuations. We propose that this ordering, which is robust in many-species models but need not be in few-species models, can be an indicator of emergent collective behavior.

Below is the code for our pH-mediated model:

import numpy as np, pandas as pd, sys, matplotlib.figure as mpfig, matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

EPS=10.**-8 ### Numerical threshold
dispersal=10**-6

def run(
       S=20, #Species number
       cp=100., #Coupling strength
       days=15,
       pH0=7,
       dilution=0.1, #if >0, daily dilution
       pc=2.5, #gate width
       kgrowth=10., #growth rate
       **kwargs
           ):

   ppref=kwargs.get('ppref',np.random.uniform(pH0-pc,pH0+pc,S))
   cs= kwargs.get('cs',np.random.uniform(-1,1,S)*cp )
   x0=kwargs.get('x0',np.concatenate([[pH0],np.log(np.random.random(S)*0.01)]) )

   def fun(p):
       ingate=(np.abs(p-ppref)<pc ).astype('float')
       return  ingate

   def eqs(t,x):
       p=x[0]
       x=np.exp(np.clip(x[1:],np.log(EPS),0))
       dx= x * (1-x)* kgrowth*fun(p) 
       if dilution<0:
           #Continuous-time dilution
           dx+= np.log(-dilution)*x                
       dx+= dispersal
       dp=np.sum(cs*x) 
       if dilution<0:
           dp+= np.log(-dilution)*(p-pH0)
       if p>14:
           dp=min(0,dp)
       if p<0:
           dp=max(0,dp)
       return np.concatenate([[dp],dx/x])
   
   time=[]
   pH=[]
   Ns=[]
   for day in range(days):
       sol=solve_ivp(fun=eqs, t_span=(0,1.),y0=x0)
       pH=np.concatenate([pH,sol.y[0]])
       if len(Ns):
           Ns=np.concatenate([Ns,np.exp(sol.y[1:].T)])
       else:
           Ns=np.exp(sol.y[1:].T)
       time=np.concatenate([time,sol.t+day])
       x0=sol.y[:,-1].copy()
       if dilution>0:
           #Discrete daily dilution
           x0[0]=(1-dilution)*pH0 + dilution* x0[0]
           x0[1:]=np.clip(x0[1:]+np.log(dilution),np.log(EPS),None)
   return time[:-1],pH[:-1],Ns[:-1]

def measure(ts,pH,Ns):
   Nf=Ns[-1]
   S=len(Nf)
   days=sorted(set(ts//1))
   
   observation_period=int(max(days))//3
   Nmean=np.array([ np.mean(Ns[ts//1 ==z],axis=0) for z in days ])
   nrel=Nmean/np.sum(Nmean,axis=1).reshape((-1,1))
   pHmean=np.array([ np.mean(pH[ts//1 ==z]) for z in days ])
   Ntot=np.sum(Nmean,axis=1)

   alive=np.where(Nmean[-1]>dispersal*S)[0]
   nalive=len(alive)

   CV=np.std(Nmean[-observation_period:,alive],axis=0)/(0.01+np.mean(Nmean[-observation_period:,alive],axis=0))
   meanCV=np.mean(CV)
   fluct=(meanCV > 0.25)
   
   return {'alive':float(nalive)/S,'fluct':float(fluct),}

Ss=[1,2,3,4,6,8,10,12,15,18,21,24,30,36,42,48]
cps=np.logspace(0,4,13)
replicas=500
days=20
table=[]
dilution=-0.033

fname='pHdata.csv'
df=None
for S in Ss:
   for cp in cps:
       print 'RUN:', S, cp
       nrep=replicas
       if S==Ss[-1]:
           nrep=replicas*2
       for replica in range(nrep):
           print '         ',replica
           opts={'days':days,'cp':cp,'dilution':dilution,}
           ts,pH,Ns=run(S=S,**opts)  
           dic={'S':S, 'cp':cp,'replica':replica}
           dic.update(measure(ts,pH,Ns))
           table.append(dic)
df=pd.DataFrame(table)  
df.to_csv(fname)