Measurement of the Translational Diffusion Coefficient and Hydrodynamic Radius of Proteins by Dynamic Light Scattering

Background

Diffusion is a process whereby solute concentration differences spontaneously decrease toward a state of homogeneity. It is a fundamental process in biological systems that governs the molecular collisions that drive biochemical reactions and intracellular transport (Berg, 1983). Strictly speaking, this process is called translational diffusion in contrast to the rotational diffusion of particles. An empirical law describing one-dimensional diffusion was described by Fick in the 19^th century, which states that the rate of flow of particles is proportional to the concentration gradient at a given position. The proportionality constant is called the diffusion coefficient, D.

A molecular interpretation of diffusion was made by Einstein in a series of papers beginning in 1905 (Einstein, 1926 [English translation first]). Einstein proposed that solute particles are subjected to forces due to collisions with solvent particles that are in random, Brownian motion due to thermal energy. A particle that is accelerated by a collisional force experiences a resistive force that is proportional to the particle velocity. The proportionality constant, called the frictional coefficient, f, is a function of the size and shape of the particle. Einstein’s law of diffusion is

where k is Boltzmann’s constant and T is the absolute temperature. This equation is fundamental to the understanding of the hydrodynamic properties of macromolecules. It is important to note that it is restricted to a two-component system, e.g., a solute molecule and solvent water, in dilute solution. In a three-component system (e.g., a macromolecule, a low molecular weight electrolyte, and water), there are four diffusion coefficients, one each that components 2 and 3 would have in the absence of the other and two cross-diffusion coefficients (Tanford, 1961). In most dynamic light scattering (DLS) studies, measurements are made under so-called pseudobinary conditions, namely at low macromolecular concentration in a solution that contains an electrolyte at sufficiently high concentration to screen the charge of the macromolecule. Under these conditions, cross-diffusion terms are considered negligible.

For a spherical particle with radius R, Stokes’ law is

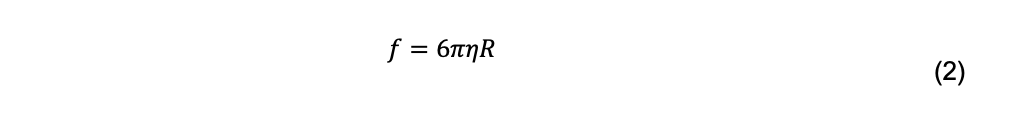
where η is the solvent viscosity. Combined with the Einstein equation, the radius of a spherical particle can be calculated if its diffusion coefficient is measured in a solution with known temperature and viscosity
                   

For a particle with arbitrary shape, the hydrodynamic radius, R_h (also called the Stokes radius), can be calculated using the Stokes-Einstein equation

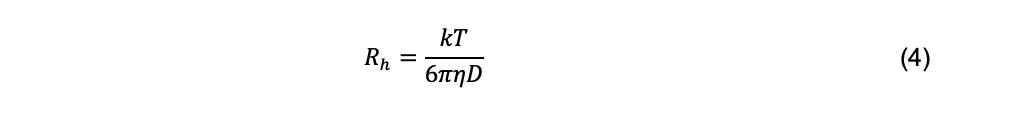
The hydrodynamic radius of a particle is an abstraction defined as the radius of a hypothetical spherical particle with the same diffusion coefficient of the actual particle under consideration. It is important to recognize that “particle sizing” for non-spherical particles based on measurement of the diffusion coefficient and the Stokes-Einstein equation does not refer to any actual geometric property of the particle. R_h is used widely because of the intuitive appeal to its units of length, in contrast to the units of the diffusion coefficient, which in the cgs system are cm² s^-1. Additionally, because temperature and viscosity are components of Eq. 4, R_h is independent of temperature and viscosity if particle undergoes no structural changes over the relevant ranges of these parameters. Subject to the same caveat, diffusion coefficients are adjusted to the standard condition of 20°C in solvent water using

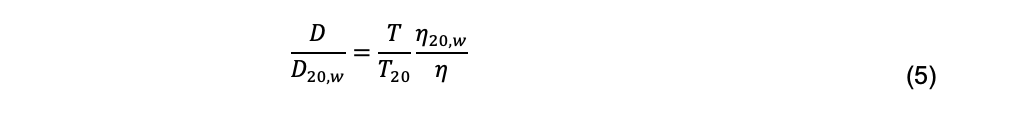
where T and T₂₀ are the absolute experimental temperature and temperature at 20°C, respectively, and η and η_20,w are the corresponding solvent viscosities (Tanford, 1961).

Diffusion measurements of particles, including macromolecules, were originally made by measuring concentration gradients (Miller, 2014). In free diffusion, a sharp boundary is formed between a solution containing particles and pure solvent in a one-dimensional diffusion cell, and the concentration gradient is measured at various positions in the cell by optical methods. The most accurate measurements have been made using Gouy interferometry and Rayleigh interferometry (Annunziata et al., 2005; Miller, 2014), which are unparalleled in accuracy and precision. While conceptually simple, free diffusion measurements are extremely demanding in practice because of the care that must be taken to avoid convective mixing, the specialized optics employed, and the analytical methods used in interpreting the interference patterns. Additionally, diffusion is relatively slow and must be allowed to proceed for hours to days to achieve a suitable concentration gradient, which limits throughput.

In contrast, diffusion measurements by DLS are easy to make, but the underlying physics is conceptually more difficult. For reviews of DLS, see references (Finsy, 1994; Stetefeld et al., 2016; Ogendal, 2017). Qualitatively, light interacts with a non-absorbing particle and is scattered quasi-elastically (i.e., at the nearly same wavelength as the incident light) in all directions. Diffusing particles can be moving either toward or away when struck by an incident photon. As a result, the scattered light is Doppler shifted to different frequencies, producing constructive and destructive interference and a fluctuating intensity. The frequency of the fluctuations increases with increasing diffusion rate, which is the underlying principle of the DLS method.

The scattered light intensity measured a short period after some arbitrary initial time is a function of the initial intensity. This relationship deteriorates as the particles randomly move about until they finally have no memory of their initial positions. The functional relationship describing the temporal dependence of the scattered light intensity due to diffusion is called autocorrelation (Berne and Pecora, 1976) and is given by the intensity autocorrelation function

where I(t) and I(t+τ) are the intensity of scattered light between an initial time t and some later time τ, called the decay time. The brackets indicate averaging over many initial times. The normalized intensity autocorrelation function is a dimensionless quantity reported by a DLS instrument and is defined as

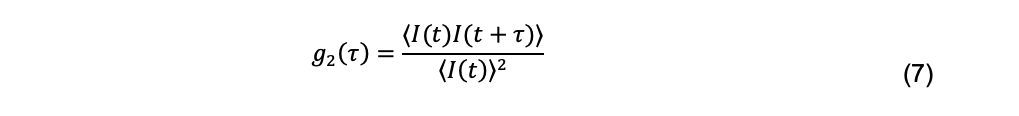
The diffusion coefficient is related to the scattered electric field, not the scattered intensity, and specifically to the normalized field autocorrelation function, defined as

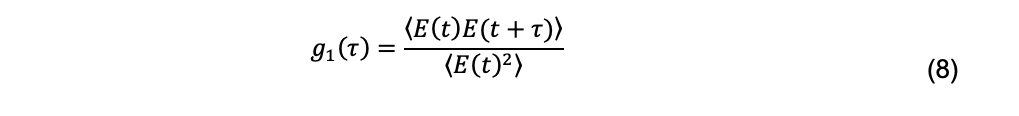
For a monodisperse system, the normalized field autocorrelation function is

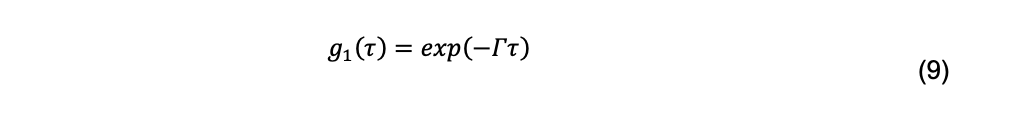
Where Γ is called the decay rate. For particles sufficiently small relative to the incident wavelength of light, the decay rate is related to the diffusion coefficient by

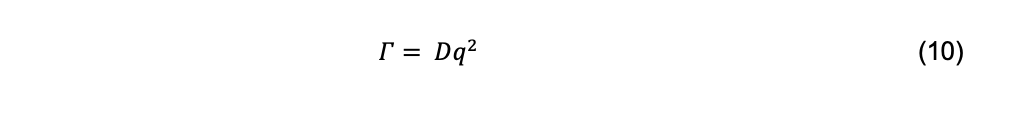
where q is the magnitude of the scattering vector,

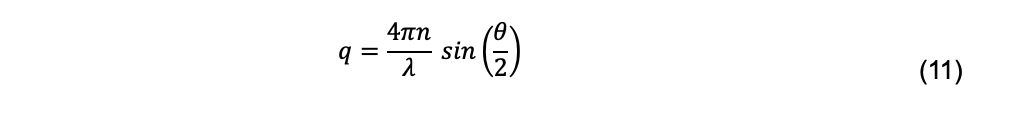
and where n is the refractive index of the solvent, λ is the wavelength of the incident light, and θ is the scattering angle.

Thus, g₂(τ) is measured, but g₁(τ) is needed to calculate a diffusion coefficient. The conversion is accomplished using the Siegert relationship

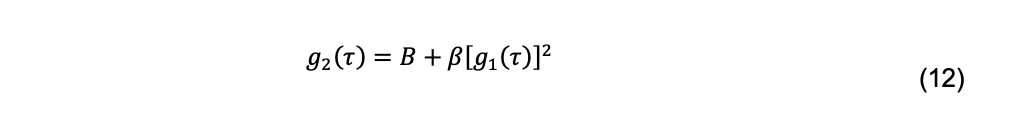
As derived B equals 1, but varies experimentally due to noise and becomes a fitted parameter. β, called the coherence factor, depends on the experimental geometry and also is a fitted parameter. Several factors complicate the interpretation of the g₂(τ) decays. Macromolecular solutions are usually polydisperse, either intrinsically (e.g., the microheterogeneity of glycoproteins) or due to impurities. Additionally, they are invariably studied as multi-component systems in the presence of salts and buffers. Scattering intensity increases approximately with the 6^th power of the hydrodynamic radius. Consequently, the presence of aggregates or other impurities larger than the particle of interest can dominate the DLS measurement. Finally, experimental noise is a feature of all measurements and is particularly troublesome in the interpretation of DLS results.

The simplest approach to deal with polydispersity is assuming some finite number, k, of scattering macromolecules and fit the data to a sum of exponential decays, producing a normalized field autocorrelation function,

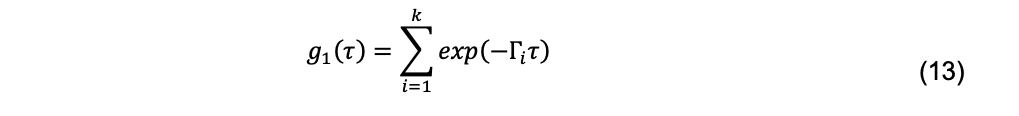
Although this is done in some fitting programs, it is more customary to assume that there is a continuous distribution of decays, G(Γ), given by

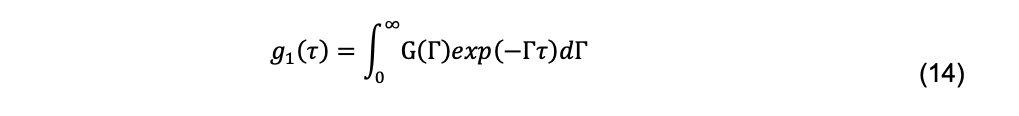
The most widely used method for fitting experimental data to this integral is cumulant analysis (Koppel, 1972). There are several methods of cumulant analysis. One approach, introduced by Frisken (2001) uses the Siegert relationship, yielding a function in which g₂(τ) vs. τ decays are fit by nonlinear least-squares regression:

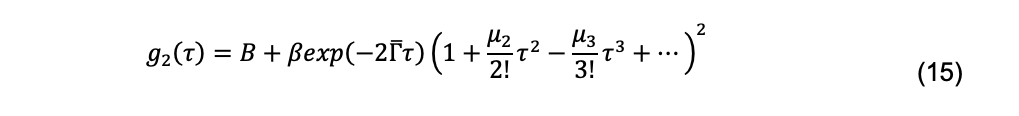
Here the mean (the first moment) of the distribution, is the z-average diffusion coefficient (Koppel, 1972),

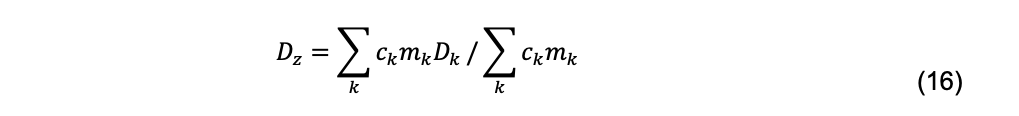
and c_k, m_k, and D_k are the total cell concentration, mass, and diffusion coefficient, respectively, of species k. μ₂, μ₃ … are the second and third moments, etc., about the mean. The second moment produces the polydispersity index,

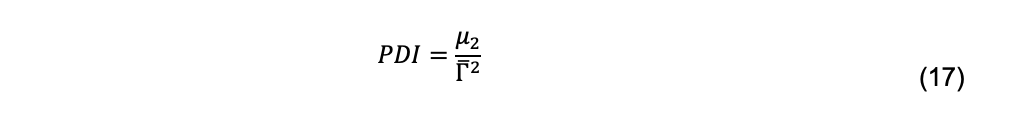
Because of measurement error, even a truly monodisperse solution will produce a non-zero estimate of μ₂. Polydispersity indices of less than 0.1 commonly are given as a criterion for monodispersity (Brautigam, 2019). Due to the errors associated with higher order moments, meaningful estimates beyond μ₂ are seldom, if ever, made.

For a monodisperse system, the molar mass, M, of a macromolecule (in cgs units of g/mol, which are used for conversion to molecular weight in daltons) can be obtained using the Svedberg equation

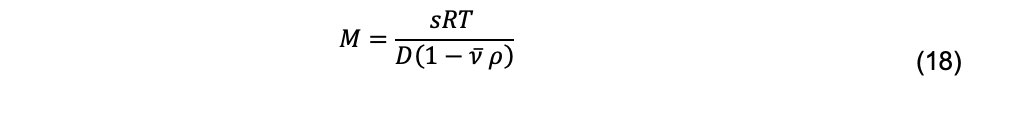
Where s and are the sedimentation coefficient and partial specific volume of the macromolecule, R is the gas constant, and ρ is the solvent density (Cantor and Schimmel, 1980). For a polydisperse system, sedimentation velocity measurements produce a weight-average sedimentation coefficient, s_w. The value of s_w, extrapolated to the condition of solvent water at 20°C and at infinite dilution, 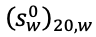, is estimated by measuring the concentration dependence of s_w and extrapolation. The corresponding value for the diffusion coefficient is 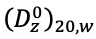. Substitution of these values in the Svedberg equation yields a weight-average molar mass, M_w, of a polydisperse system (Pusey et al., 1974).

Some authors state that cumulant analysis is only applicable to a distribution function that is Gaussian, which is incorrect. Other authors state that cumulant analysis is only applicable to monomodal functions. This also seems incorrect. However, the utility of the parameter estimates derived from a polydisperse system that produces a multi-modal is limited. For this reason, another approach is to try to fit the data to estimate the function, G(Γ), in the integral in Eq. 14, which is the distribution of all scattering particles in the system. This integral is an example of a Fredholm integral that arises in many physical systems. It does not have an analytic solution and is famously ill-posed to solve numerically. Considerable effort has been made to address the problem, and various methods are available in DLS software programs to calculate it.

Sizing and characterization of the polydispersity of “nanomaterials,” defined as particles having a “size” approximately between 1 and 100 nm (Bhattacharjee, 2016), has found application in many commercial areas. Consequently, low-cost DLS instruments featuring automated data collection and analysis have become widely available. This is both a blessing and a curse in academic applications because the non-specialist investigator has access to high quality, easy to obtain data but is intellectually far removed from the underlying technology and analysis. For example, the Malvern Zetasizer Nano S particle size analyzer, which is described in this protocol, does not even report a diffusion coefficient, but rather a hydrodynamic radius or diameter. Additionally, the documentation associated with the instrument provides limited information with respect to the properties of the instrument and methods of analysis of the experimental results.

As a result, as is often the case in the modern laboratory, in addition to the subject under study, DLS measurements open up a separate additional research project aimed towards understanding the instrument and its associated software. In this protocol, a method is described to validate a commercial DLS instrument with the goal of accurately estimating macromolecular diffusion coefficients. Bovine serum albumin (BSA) is chosen as a reference material because previous measurements have been made of its diffusion coefficient using free diffusion (Creeth, 1952 and 1958; Wagner and Scheraga, 1956) and other DLS instruments (Oh and Johnson, 1981; Gaigalas et al., 1992).