Probabilistic Models for Predicting Mutational Routes to New Adaptive Phenotypes

Equipment

1. Computer
   Any desktop computer that fulfills the system requirements for the programming language(s) used. Here a desktop computer with the following configuration was used: iMac with a 3.6 GHz Intel Core i7 processor and 16 GB 2400 MHz DDR4 memory
   

Software

1. MATLAB (MathWorks^®, http://www.mathworks.com/)
   MATLAB was used to solve the differential equations, analyze the resulting data, and generate figures. However, other programming language(s) would have sufficed so long as they can be used to numerically solve differential equations and perform simple mathematical operations, e.g., Python, Julia, Octave, or Mathematica. We note that in the associated paper (Lind et al., 2019) a combination of languages was used but for simplicity here we have put everything into a single language. MATLAB code for the procedures RunModelComparison and PlotModelComparison is available at https://github.com/ericlibby/BioProtocol.
   

Procedure

This protocol describes a method for computing the relative likelihood that a mutational change will translate into a phenotypic change in two molecular pathways. The pathways do not have to produce the same phenotype but there should be a way of determining what the phenotype is, based on the interactions between pathway components. Thus, the protocol assumes that the mechanistic details of the molecular pathways are understood; however, information may be missing concerning the reaction kinetics, the concentrations of molecular compounds, and/or the effects of mutations. This protocol outlines a procedure that randomly samples many models of the pathways and compares the likelihood that mutations in the pathway–that affect the reaction kinetics–alter the phenotype(s). The steps of the procedure are illustrated in Figure 1 using the same notation as in the text below. Figure 2 and Figure 3 presents the procedure in a pseudocode format and the full MATLAB code is available at https://github.com/ericlibby/BioProtocol.

Figure 1. Overview of modeling methodology. Details are explained in the text below using the same notation.

1. Build mathematical models of the molecular pathways that enable comparison
   1. Identify the set of biochemical reactions in each molecular pathway that determine expression of a particular phenotype. The types of reactions can vary depending on the pathway modeled and can include, for example, enzymatic reactions, conformational changes in proteins, oligomerization, and transcription initiation. The reactions should link the expression of the phenotype to some indicator, e.g., a biochemical compound (or function of compounds). For example, if the phenotype is the color of an organism then an appropriate indicator might be the amount of a pigment compound. In the article where this method was first used (Lind et al., 2019) the indicators were three diguanylate cyclase enzymes that could each be activated by mutations in their regulatory networks.
   2. For each set of biochemical reactions, formulate a system of differential equations that describes the reaction kinetics of the indicator (see Figure 1 for example). Each pathway is likely affected by biochemical compounds whose dynamics are governed by external pathways. It is often better to treat these compounds as constants rather than include more differential equations for their dynamics. For instance, if a pathway affects an indicator through phosphorylation then the intracellular pool of phosphate groups may be held as a constant rather than modeled through an additional set of differential equations. In general, it also helps to keep a similar level of detail/abstraction across the models of the pathways for better comparison. As an example, in (Lind et al., 2019) the models of the different pathways focused on the interactions between proteins and ignored processes involving transcription.
      
      
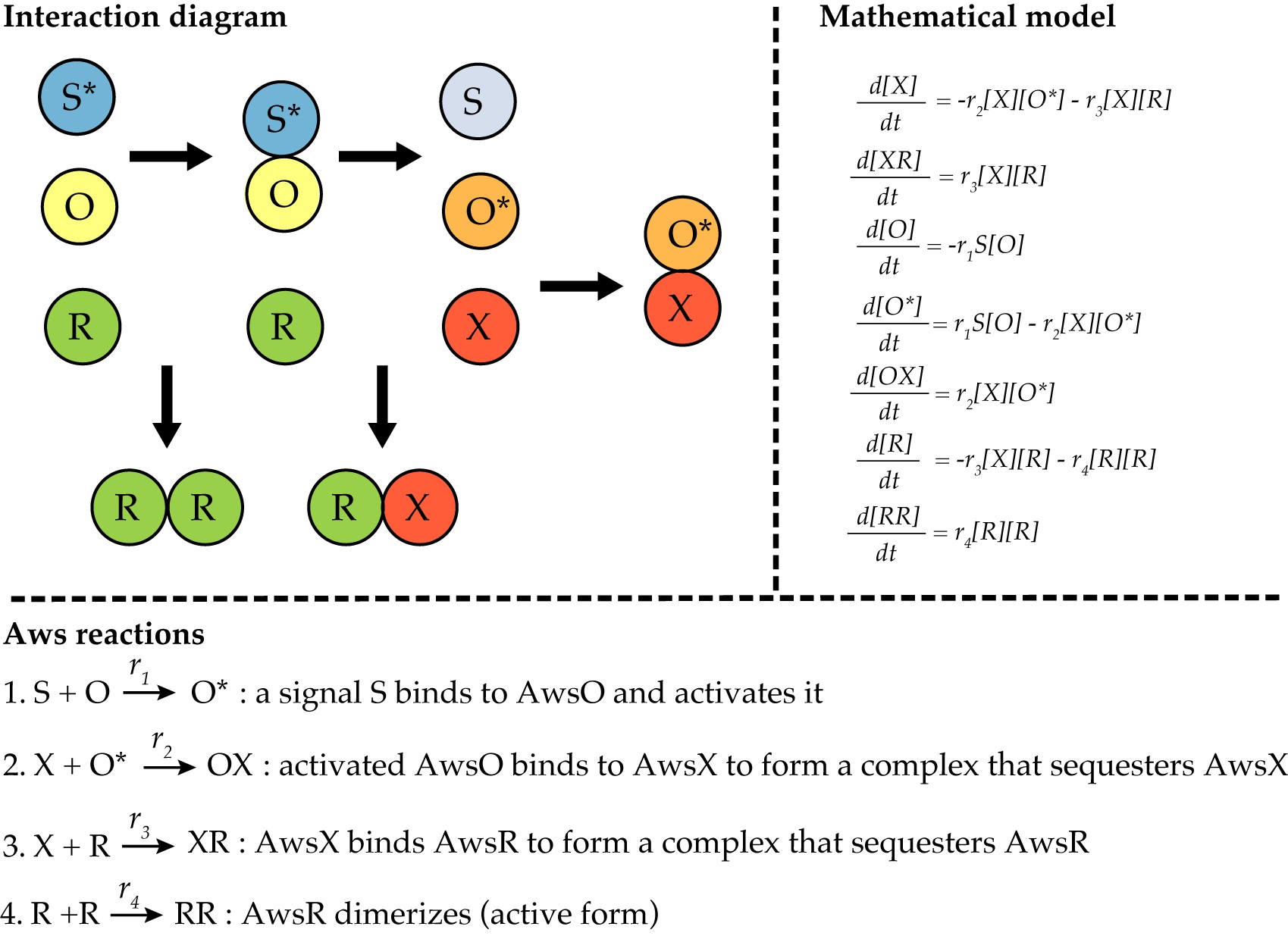
      Figure 2. Modeling of the AWS network. The reactions of the AWS regulatory network from (Lind et al., 2019) can be illustrated by an interaction diagram. The mathematical model of AWS is a system of ordinary differential equations describing all reactions and rates. In this case, the active dimer RR is the indicator of phenotypic change.
      
   
   
2. Choose parameter distributions to solve the differential equations
   We assume that the systems of differential equations used to model the pathways cannot be solved analytically. To solve each system of differential equations numerically, three key pieces of information are needed:
   1. Initial concentrations of the molecular compounds.
   2. Reaction rates for the interactions between compounds.
   3. Time interval over which to solve the differential equations.
   It is possible that all pieces of information are known for a model in which case there will be only one numerical solution for each pathway model. In most cases, however, information is missing and must be estimated. 
   
   
   1. If there is any information concerning a) or b) that is known or can be estimated from empirical data then use this to constrain the sampling procedure. For unknown concentrations or reaction rates, choose a distribution for each that seems reasonable based on empirical data or at least encompasses a broad spectrum of likely dynamics. For instance, in Lind et al. (2019) there was no information concerning reaction rates or concentrations, so the authors chose the distribution for the reaction rates to be a uniform distribution on log space (i.e., 10^U[−2,2]) and the distribution for initial concentrations to be a uniform distribution U[0,10]. These choices were in line with other pathway reaction kinetic models and allowed for numerically stable solutions. Importantly, whatever distributions are chosen, it is useful to see the effects of different choices on the results of the pathway comparison as part of a post-analysis parameter sensitivity study.
   2. The time interval for numerical solving the differential equations depends on the particular molecular system and the dynamics of the indicator compound. If the indicator reaches a steady state then that might set the time interval; however, in some systems transient, short-term behavior may be more biologically relevant. A distribution could be chosen for the time to solve the differential equations; however, in practice it is often faster and easier to evaluate the results when a fixed time is chosen and used for all models–especially when all other parameters are sampled randomly.
   
   
3. Choose distributions for the effects of mutations and the amount of change in the indicator compound that corresponds to phenotypic change
   The prior steps allow for the computation of the indicator compound in each pathway, as a baseline for comparison. The choices made in this step will allow numerical solution of a pathway’s differential equation model following a mutation (or set of mutations) and determination of whether the phenotype has changed.
   1. We assume that the relevant mutations to a pathway are those that alter reaction rates, i.e., change the internal dynamics of a pathway, and we classify mutations as enabling or disabling based on whether they increase/decrease reaction rates. Thus, we need a way of determining new reaction rate(s) in the differential equation model of a pathway, following a mutation (or a set of mutations). Ideally, one would have information on all possible mutations and their effects on reaction rates. However, this is unlikely to be available. In the absence of empirical data, a distribution should be picked such that given a reaction rate and whether a mutation increases or decreases reaction rates, a new reaction rate is determined. For example, in (Lind et al., 2019) enabling mutations were assumed to affect reaction rates multiplicatively and thus new reaction rates were computed as the product of the original reaction rate and a multiplicative factor sampled from 10^U[0,2] (similarly a factor of 10^U[−2,0]) was used for disabling mutations. 
   2. The differential equation models for each pathway link the concentration of an indicator compound to a phenotype. Since the sampling distributions in Step B may result in different baseline concentrations of indicator compound, there needs to be a way of assessing whether a mutation (or set of mutations) produces a phenotypic change. In the absence of empirical data, a simple approach is to establish that if the indicator increases in concentration above some threshold then the phenotype changes. The actual threshold will depend on the biological system and how much of a change in the indicator is biologically relevant. Without this information, the threshold should be high enough to avoid issues of numerical precision and will depend on the differential equation solver and its parameters (e.g., step sizes in Runge-Kutta methods). For simplicity, we used a threshold of 0.000001 which was similar in magnitude to the numerical tolerances used in the differential equation solver.
   
   
4. Run simulation routine to compute the likelihood of a phenotypic change given all combinations of mutations
   Use the code “Run Model Comparison” (https://github.com/ericlibby/BioProtocol/blob/master/RunModelComparison.m) to generate the data. The pseudocode for “Run Model Comparison” is included below as Algorithm 1 (Figure 3). “Run Model Comparison” use the procedure “Phenotype Change” for each pathway to compute the probability that mutation in a pathway causes a phenotypic change. The pseudocode for “Phenotype Change” is shown in Figure 3. “Phenotype Change” uses several procedures to set the parameter distributions (Procedure B, C above). The pseudocode for these are shown in Figure 4. To visualize the results, use the code “Plot Model Comparison” (https://github.com/ericlibby/BioProtocol/blob/master/PlotModelComparison.m) to create a contour plot that shows the log₂ ratio of relative probabilities between two pathways with axes denoting the probabilities of enabling and disabling change.
   
   
   Figure 3. Pseudocode for the “RunModelComparison” and “PhenotypeChange” procedures. “PhenotypeChange” compute the probability that mutation in a pathway causes a phenotypic change. “RunModelComparison” computes the relative likelihood that Pathway 1 is used relative to Pathway 2. MATLAB code for RunModelComparison is available at https://github.com/ericlibby/BioProtocol/blob/master/RunModelComparison.m.
   
   
   Figure 4. Pseudocode for procedures used by “PhenotypeChange” procedure shown in Figure 3. The SolveModel procedure is not listed as it is assumed to be a numerical solver available as a built-in function or from a library/package.
   

Data analysis

The result of running the codes “Run Model Comparison” (https://github.com/ericlibby/BioProtocol/blob/master/RunModelComparison.m) and “Plot Model Comparison” (https://github.com/ericlibby/BioProtocol/blob/master/PlotModelComparison.m) is a contour plot that shows the ratio of likelihoods that the pathways produce a phenotypic change for different values of the probabilities of enhancing and disabling mutations (the vertical and horizontal axes, respectively). In terms of statistical analyses, it depends on the conclusions that are drawn. The contour plot only shows the ratio of the average likelihood for each pathway. Further analyses can investigate the standard deviation or maximum/minimum of the likelihoods. We recommend that additional analyses be performed to validate any conclusions. In particular, the analyses can be performed again with changes to the probability distributions to test for parameter sensitivity. Alternatively, the number of iterations can be increased/decreased by some factor to evaluate whether the contour plot remains stable. Examples of these analyses can be found in Figure 5 and associated methods of Lind et al., 2019.

Acknowledgments

This protocol was adapted from (Lind et al., 2019).

Competing interests

The authors declare no competing financial interest.

References

1. Bocci, F., Suzuki, Y., Lu, M. and Onuchic, J. N. (2018). Role of metabolic spatiotemporal dynamics in regulating biofilm colony expansion. Proc Natl Acad Sci U S A 115: 4288-4293.
2. Bromberg, Y. and Rost, B. (2007). SNAP: predict effect of non-synonymous polymorphisms on function. Nucleic Acids Res 35(11): 3823-3835.
3. Capriotti, E., Calabrese, R., Fariselli, P., Martelli, P. L., Altman, R. B. and Casadio, R. (2013). WS-SNPs&GO: a web server for predicting the deleterious effect of human protein variants using functional annotation. BMC Genomics 14 Suppl 3: S6.
4. Capriotti, E., Fariselli, P. and Casadio, R. (2005). I-Mutant2.0: predicting stability changes upon mutation from the protein sequence or structure. Nucleic Acids Res 33(Web Server issue): W306-310.
5. Celniker, G., Nimrod, G., Ashkenazy, H., Glaser, F., Martz, E., Mayrose, I., Pupko, T. and Ben-Tal, N. (2013). ConSurf: using evolutionary data to raise testable hypotheses about protein function. Isr J Chem 53: 199-206.
6. Chandrasekaran, S. and Price, N. D. (2010). Probabilistic integrative modeling of genome-scale metabolic and regulatory networks in Escherichia coli and Mycobacterium tuberculosis. Proc Natl Acad Sci U S A 107: 17845-17850. 
7. Choi, Y. and Chan, A. P. (2015). PROVEAN web server: a tool to predict the functional effect of amino acid substitutions and indels. Bioinformatics 31(16): 2745-2747.
8. Dehouck, Y., Kwasigroch, J. M., Gilis, D. and Rooman, M. (2011). PoPMuSiC 2.1: a web server for the estimation of protein stability changes upon mutation and sequence optimality. BMC Bioinformatics 12: 151. 
9. Edwards, J. S. and Palsson, B. O. (2000). Metabolic flux balance analysis and the in silico analysis of Escherichia coli K-12 gene deletions. BMC Bioinformatics 1: 1.
10. Kumar, P., Henikoff, S. and Ng, P. C. (2009). Predicting the effects of coding non-synonymous variants on protein function using the SIFT algorithm. Nat Protoc 4(7): 1073-1081. 
11. Lind, P. A. (2018). Evolutionary forecasting of phenotypic and genetic outcomes of experimental evolution in Pseudomonas. bioRxiv. 342261.
12. Lind, P. A., Arvidsson, L., Berg, O. G. and Andersson, D. I. (2017). Variation in mutational robustness between different proteins and the predictability of fitness effects. Mol Biol Evol 34(2): 408-418.
13. Lind, P. A., Farr, A. D. and Rainey, P. B. (2015). Experimental evolution reveals hidden diversity in evolutionary pathways. Elife 4: e07074.
14. Lind, P. A., Libby, E., Herzog, J. and Rainey, P. B. (2019). Predicting mutational routes to new adaptive phenotypes. Elife 8: e38822.
15. Liu, J., Prindle, A., Humphries, J., Gabalda-Sagarra, M., Asally, M., Lee, D. Y., Ly, S., Garcia-Ojalvo, J. and Suel, G. M. (2015). Metabolic co-dependence gives rise to collective oscillations within biofilms. Nature 523(7562): 550-554. 
16. Luksza, M. and Lassig, M. (2014). A predictive fitness model for influenza. Nature 507(7490): 57-61.
17. McCandlish, D. M. and Stoltzfus, A. (2014). Modeling evolution using the probability of fixation: history and implications. Q Rev Biol 89(3): 225-252.
18. Neher, R. A., Russell, C. A. and Shraiman, B. I. (2014). Predicting evolution from the shape of genealogical trees. Elife 3: e03568.
19. O'Brien EJ, Monk JM, Palsson BO. (2015). Using Genome-scale Models to Predict Biological Capabilities. Cell 161:971-987.
20. Yates, C. M., Filippis, I., Kelley, L. A. and Sternberg, M. J. (2014). SuSPect: enhanced prediction of single amino acid variant (SAV) phenotype using network features. J Mol Biol 426(14): 2692-2701.